🔢鱼C算法课堂-note
说明:
本笔记是根据该视频记录的个人笔记...
一、百钱百鸡
本节:
【 方程组 | 穷举法 | 循环 | 优化 】
题目:
已知 :其中一只公鸡5元,一只母鸡3元,3只小鸡算1元
请问:现要用100元买100只鸡,公鸡、母鸡、小鸡各能买几只?
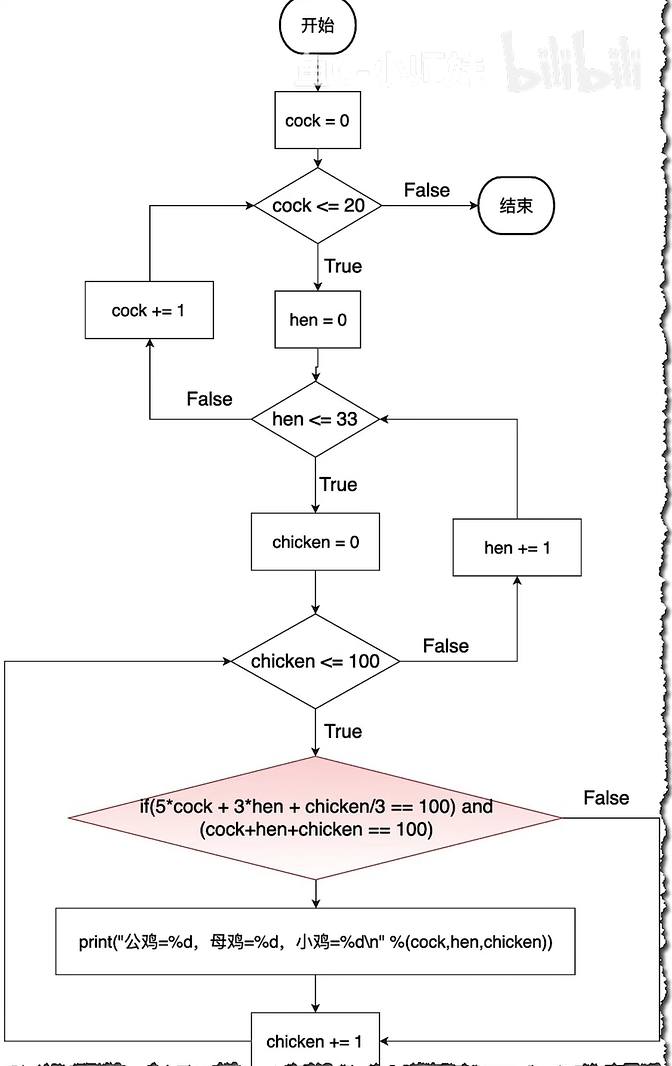
思考:如果100元全部买公鸡可买20只,全部买母鸡可以买33只,全部买小鸡可以买100只
使用变量
cock存储公鸡数量,hen存储母鸡数量,chicken存储小鸡数量那么可以发现约束条件:
数量约束:
cock + hen + chicken == 100价格约束:
5 * cock + 3 * hen + chicken / 3 == 100
思路:我们只需要遍历出每一种情况,然后满足约束条件的就是答案(穷举法)
流程图:
代码:
python# 注意range是前开后闭的区间 for cock in range(0, 21): # cock范围0-20 for hen in range(0, 34): # hen范围0-33 for chicken in range(0, 101): # chicken范围0-100 if (cock + hen + chicken == 100) and \ (5 * cock + 3 * hen + chicken / 3 == 100): print(f"cock = {cock} hen = {hen} chiken = {chicken}")运行结果:
textcock = 0 hen = 25 chiken = 75 cock = 4 hen = 18 chiken = 78 cock = 8 hen = 11 chiken = 81 cock = 12 hen = 4 chiken = 84
💡小结(穷举法):
对于一个会出现多种情况,而我们要根据约束筛选出特定情况的问题,在情况数量不算特别多的情况下(考虑python效率不高,数量太多会运行时间很长),我们通常可以考虑使用 穷举法 去暴力破解:
- 使用嵌套循环遍历出各种情况
- 在最内层循环可以收集到各种情况,所以我们在最内层写 if 逻辑筛选
- 根据题目描述,找全约束条件,可以用 嵌套if 或者 if 配合逻辑运算符 写全所有约束条件
- 在 if 条件满足的语句体内打印满足所有约束条件的情况
二、找女神手机号
本节:
【 流程图 | for...in range() 】
题目:
已知 :女神手机尾号为一个四位数,前两位数字相同,后两位数字相同,
前两位数字与后两位数字互不相同,并且这个四位数是一个整数的平方值。
求:女神手机尾号这四位数是什么?
题目分析:
- 手机尾号为一个四位数:设每一位为 a,b,c,d, 取值范围 [0,9]
- 前两位数字相同:a = b ( 结合1.“为一个四位数” :a = b ≠ 0 )
- 后两位数字相同:c = d
- 前两位数字与后两位数字互不相同:a ≠ c
- 这个四位数是一个整数(设为 t )的平方: 1000a + 100b +10c + d == t * t
我们还是可以通过构造嵌套循环使用穷举法来暴力破解:
把前两位数字使用变量 i 表示,后两位数字用变量 j 表示
那个整数使用 t 表示 , t 的平方使用 k 表示 ,即 k 也就是那个四位数
进一步分析,四位数的最小值为 1100 ,而 33 的平方值为 1089
所以我们可以知道 t 的取值范围是 [ 34 , 99 ] , 这样可以节省我们遍历的次数
使用 for 循环编写代码:
python# range(10)生成的列表是 0-9 (10个数) for i in range(10): # 前两位数 for j in range(10): # 后两位数 if (i != j): # 前两位数字与后两位数字互不相同 k = 1000 * i + 100 * i + 10 * j + j # k表示四位数取值 for t in range(34, 100): # 整数 t 的取值范围是 34-99 if (k == t * t): print("女神手机号后四位:",k)运行结果:
text女神手机号后四位: 7744while循环版代码:
pythoni = 1 while i <= 9: j = 0 while j <= 9: if (i != j): k = 1000 * i + 100 * i + 10 * j + j t = 34 while t <= 99: if (k == t * t): print(k) t += 1 j += 1 i += 1
三、借玩具
本节:
【 循环三要素 | 字符串格式化 】
题目:
已知 :小由鱼到手了5个新玩具,准备借给3位鱼油一起分享快乐,一位鱼油只分一个玩具
请问:共有几种不同的分配情况
题目分析:
3个鱼油:分别使用 A , B , C 来表示
5个新玩具:使用 玩具1 - 玩具5来表示,且用变量 a , b , c 分别存储 ABC三人拿到的玩具序号
可以发现:这种题目就是数学中常见的 “排列组合” 问题
我们还是可以使用 穷举法来暴力破解它:
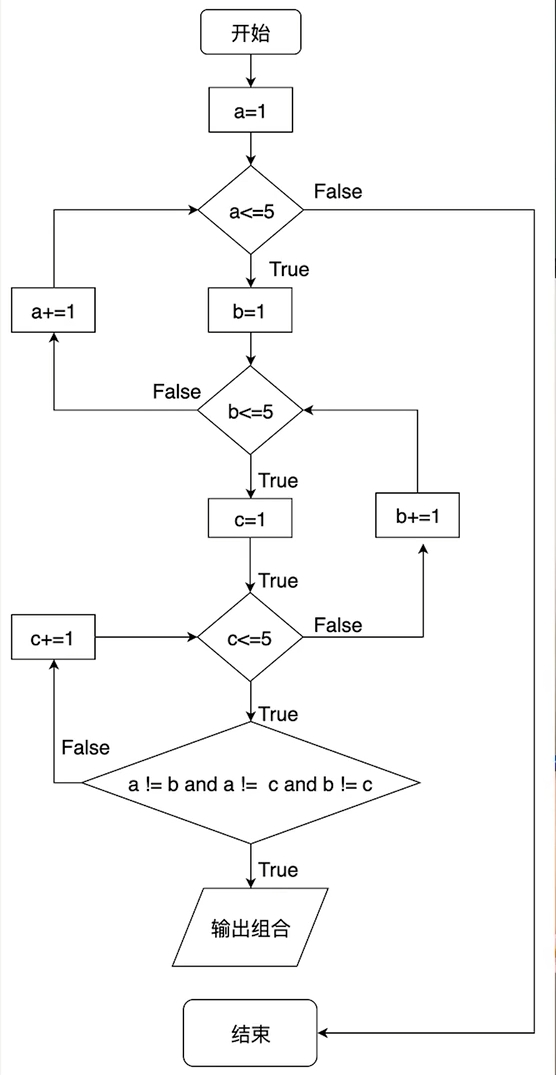
- 使用三层嵌套循环分别遍历a,b,c,取值范围是1-5( 即range(1,6) )
- 在最内层循环就会获得全部情况的组合,这样我们没经过筛选就会出现取到玩具序号相同的情况
- 在最内层写 if 筛选掉取到玩具序号相同的情况
- 即约束条件为
(a != b) and (a != c) and (b != c)
流程图:
编写代码:
pythonfor a in range(1, 6): for b in range(1, 6): for c in range(1, 6): if (a != b) and (a != c) and (b != c): print("A:玩具%d B:玩具%d C:玩具%d" % (a,b,c))输出结果:
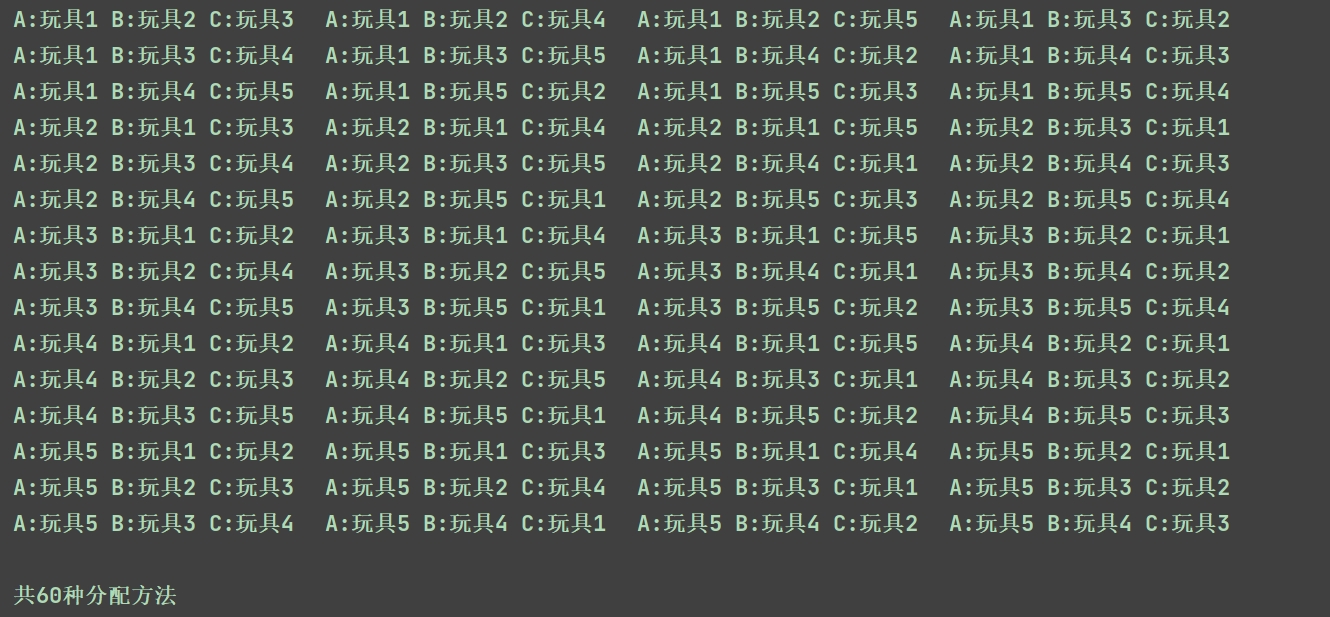
textA:玩具1 B:玩具2 C:玩具3 A:玩具1 B:玩具2 C:玩具4 A:玩具1 B:玩具2 C:玩具5 A:玩具1 B:玩具3 C:玩具2 A:玩具1 B:玩具3 C:玩具4 ... ...其实我们还可以对输出结果进行优化:
输出结果没有打印题目要的答案 “共有几种不同的分配情况” ,难道要我们自己数吗?
输出样式不好看,换行太多, 一种情况就占据一行了
对于情况一:我们可以在最外层添加一个count变量进行计数,每找到一次有效组合count加一
代码改进一:
pythoncount = 0 for a in range(1, 6): for b in range(1, 6): for c in range(1, 6): if (a != b) and (a != c) and (b != c): print("A:玩具%d B:玩具%d C:玩具%d" % (a,b,c)) count += 1 print(f"共{count}种分配方法")输出结果:
textA:玩具1 B:玩具2 C:玩具3 A:玩具1 B:玩具2 C:玩具4 A:玩具1 B:玩具2 C:玩具5 ... A:玩具5 B:玩具4 C:玩具2 A:玩具5 B:玩具4 C:玩具3 共60种分配方法
对于情况二:我们可以利用count来进行换行,如每 4个换一行
代码改进二:
pythoncount = 0 for a in range(1, 6): for b in range(1, 6): for c in range(1, 6): if (a != b) and (a != c) and (b != c): # print()的end参数默认是换行,即\n # 我们改成\t(即一个制表符),正常打印我们不让他换行,下面用count控制换行 print("A:玩具%d B:玩具%d C:玩具%d" % (a,b,c),end="\t") count += 1 if (count % 4 == 0): print() # 每4个换一次行 print() print(f"共{count}种分配方法")输出结果:
💡小结:
1. 循环三要素
- 循环变量的初值
- 循环的控制条件
- 循环趋于结束的循环变量值的改变
在c语言的for循环里,括号填入的三个值刚好就是上述三个
- c
//c语言for循环语法 for ( init; condition; increment ) { statement(s); }
2. 字符串格式化
Python 中有三种格式化操作符,分别是 format 、%s 、 f 。
2_1. format
此函数可以快速的处理各种字符串,增强了字符串格式化的功能。
基本语法是使用{}和.format()。format函数可以接受不限各参数,位置可以不按照顺序
name = '张三'
age = 18
nickname = '法外狂徒'
# format 用 {} 占位
print('姓名:{},年龄{},外号:{} '.format(name, age, nickname))
# 姓名:张三,年龄18,外号:法外狂徒
print('hello {aa} 你今年已经{bb}岁了'.format(bb = age,aa = name))
# hello 张三 你今年已经18岁了2_2. f
f'{}'形式,并不是真正的字符串常量,而是一个运算求值表达式,
可以很方便的用于字符串拼接、路径拼接等
name = '张三'
# f 在字符串中嵌入变量
print(f'hello {name} !')
# hello 张三 !%s
%被称为格式化操作符,专门用于处理字符串中的格式
- 包含
%的字符串,被称为格式化字符串%和不同的字符连用,不同类型的数据需要使用不同的格式化字符
| 格式化字符 | 含义 |
|---|---|
| %s | 字符串 |
| %d | 有符号十进制整数,%06d 表示输出的整数显示位数,不足的地方使用0补全 |
| %f | 浮点数,%.2f 表示小数点后只显示两位 |
| %% | 输出 % |
| %c | %ASCII字符 |
| %o | %8进制 |
| %x | %16进制 |
| %e | %科学计数法 |
语法格式如下
pythonprint("格式化字符串 %s" % '变量1') print("格式化字符串" % ('变量1', '变量2', ...))pythonname = '张三' age = 18 nickname = '法外狂徒' name2 = '李四' age2 = 19 nickname2 = '帮凶' # %s 用 %s 占位 print('姓名:%s' % name) # 姓名:张三 # 多个参数 print('%s,%s 哦嗨呦' % (name, name2)) # 张三,李四 哦嗨呦
🚩拓展 (itertools模块)
像刚刚的题目:
已知 :小由鱼到手了5个新玩具,准备借给3位鱼油一起分享快乐,一位鱼油只分一个玩具
请问:共有几种不同的分配情况
一看就是数学中的那种
A53的排列问题
ps : 先选后排 ,有5个玩具,选出三个来
C53, 又因为要分给ABC三个鱼油,所以是有顺序的,再乘
A33, 那其实综合起来就可以写成是A53,一共60种,也符合之前算的结果调用
from itertools import permutations
代码改进:
python# 代码改进 from itertools import permutations count = 0 for a,b,c in permutations(range(1,6),r=3): print("A:玩具%d B:玩具%d C:玩具%d" % (a, b, c)) count += 1 print(f"共{count}种分配方法")输出结果:
textA:玩具1 B:玩具2 C:玩具3 A:玩具1 B:玩具2 C:玩具4 A:玩具1 B:玩具2 C:玩具5 ... A:玩具5 B:玩具4 C:玩具2 A:玩具5 B:玩具4 C:玩具3 共60种分配方法这可简洁了不少啊!
四、兑换钱币
本节:
【 N-S图 | range()函数 】
题目:
已知 :将50元的猛男币兑换成10元、5元和1元的钱币
请问:一共有多少种不同的兑换方法呢?
题目分析:
一个猛男币值50元,问刚好可以换成10元,5元,1元的组合
可以把 10元钱币,5元钱币,1元钱币分别取的价格数设为
x,y,z
全用10元钱币,可以取到的价格为
[0,10,20,30,40,50]全用5元钱币,可以取到
[0,5,10,15,...,50]全用1元钱币 ,可以取到
[0,1,2,3,...,50]约束条件:
if (x + y + z == 50), 即 三种钱币的总价格刚好50元
所以我们还是用最简单的穷举法先写出第一版本的代码:
pythoncount = 0 for x in range(0, 51, 10): # 10元钱币可取值[0,10,20,30,40,50] for y in range(0, 51, 5): # 5元钱币可取值[0,5,10,15,...,50] for z in range(0, 51): # 1元钱币可取值[0,1,2,3,...,50] if (x + y + z == 50): print(f"10元{x//10}张,5元{y//5}张,1元{z}张") count += 1 print(f"共有{count}种不同的兑换方法")输出结果:
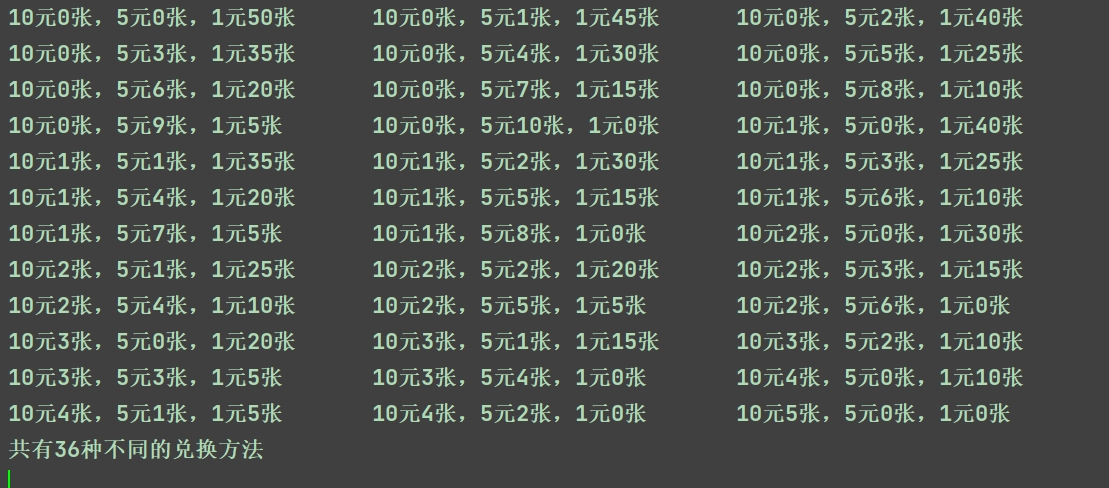
text10元0张,5元0张,1元50张 10元0张,5元1张,1元45张 10元0张,5元2张,1元40张 ... 10元4张,5元1张,1元5张 10元4张,5元2张,1元0张 10元5张,5元0张,1元0张 共有36种不同的兑换方法
然后还是输出太长,一样用之前判断count变量的方式,使它少点换行
python# 换行版本 count = 0 for x in range(0, 51, 10): # 10元钱币可取值[0,10,20,30,40,50] for y in range(0, 51, 5): # 5元钱币可取值[0,5,10,15,...,50] for z in range(0, 51): # 1元钱币可取值[0,1,2,3,...,50] if (x + y + z == 50): # 找到满足条件的就先计数加一 count += 1 # 然后进行换行判断 if count % 3 == 0: # 刚好够3个一行就打印换行版本的print语句 print(f"10元{x // 10}张,5元{y // 5}张,1元{z}张") else: # 其余情况用制表符空开 print(f"10元{x // 10}张,5元{y // 5}张,1元{z}张", end="\t\t") print(f"共有{count}种不同的兑换方法")输出结果:
这样格式好多了~
可以发现,这种题目的场景就是
itertools模块里面的笛卡尔积有多个集合,里面的元素分别进行一 一的组合
from itertools import productproduct(*iterables,repeat=1)
使用笛卡尔积对代码进行改写:
python# 使用笛卡尔积 from itertools import product count = 0 # 10元钱币可取值[0,10,20,30,40,50],即0到5张 ten_yuan_values = range(0, 51, 10) # 5元钱币可取值[0,5,10,15,...,50],即0到10张 five_yuan_values = range(0, 51, 5) # 1元钱币可取值[0,1,2,3,...,50],即0到50张 one_yuan_values = range(0, 51) # 使用itertools.product生成所有可能的组合 for x, y, z in product(ten_yuan_values, five_yuan_values, one_yuan_values): if x + y + z == 50: print(f"10元{x//10}张,5元{y//5}张,1元{z}张") count += 1 print(f"共有{count}种不同的兑换方法")
五、与谁结婚
本节:
【 逻辑推断 | 条件组合 】
题目:
已知 :有三对情侣要结婚啦,三位靓仔A ,B , C,和三位小仙女 X ,Y, Z。这三对情侣比较皮,准备让吃瓜路人小由鱼来猜谁和谁要结婚。小由鱼为了配对成功,询问了其中三位,得到的回答是:
A 说他要和 X 结婚; X说她的未婚夫是C ; C 说他要和 Z 结婚;
听到这样的回答,小由鱼知道他们都是在开玩笑,说的都是假话!!
请求:帮小由鱼找出谁和谁要结婚...
题目分析:
三位靓仔A ,B , C, 和 三位小仙女 X ,Y, Z
还有三句假话:A 说他要和 X 结婚; X说她的未婚夫是C ; C 说他要和 Z 结婚;
先定义一个boy列表
['A','B','C'], 然后用变量 x , y , z 存储三个小仙女的对象根据假话来写出约束条件:
- A的新娘不是X --->
x! = A- 与X结婚的不是C -->
x! = C- C的新娘不是Z -->
z! = C- 区分 x , y , z 三个人 ,三人与 A,B, C,一 一 对应 :
x != yx != zy != z把上述约束条件组合起来就能找到xyz三个变量所满足的条件对应的结果。
那么我们可以用逻辑运算符串出总条件:
x!=boy[0] and x!=boy[2] and z!=boy[2] and x!=y and x!=z and y!=z那么我们就可以在程序中用三重循环来穷举出xyz的所有值,然后在最内层放上这个约束
符合这个约束的再打印出来,那个就是正确的组合了!
使用穷举法编写代码:
python# 定义一个boy列表 boy = ['A','B','C'] # 用变量 x , y , z 存储三个小仙女的对象 for x in boy: for y in boy: for z in boy: if(x!=boy[0] and x!=boy[2] and z!=boy[2] and x!=y and x!=z and y!=z): print(f"结果是X与{x}结婚,Y与{y}结婚,Z与{z}结婚")运行结果:
text结果是X与B结婚,Y与C结婚,Z与A结婚
使用
itertools改写代码:观察上述情景,可以理解成是有顺序的让 ABC
排列,对应到xyz上符合约束条件的一组排列才是正确的排列,所以应该用
permutationspython# 使用itertools改写代码 from itertools import permutations boy = ['A','B','C'] # 用变量 x , y , z 存储三个小仙女的对象 for x,y,z in permutations(boy,r=3): if (x != boy[0] and x != boy[2] and z != boy[2] and x != y and x != z and y != z): print(f"结果是X与{x}结婚,Y与{y}结婚,Z与{z}结婚")运行结果:
text结果是X与B结婚,Y与C结婚,Z与A结婚