🐍蓝桥py组_Note
一、递归
递归的两个条件:
- 调用自身
- 结束条件
下面用四个简单的例子来说明,辨别下列是否为递归
对于
func1,这并不是一个递归,它满足了调用自身,但不满足结束条件,因为在
x-1不断执行下去, x 是可以不断接近 负无穷的,没有终止条件
对于
func2也是只有调用自身,而无结束条件,虽然有 if 判断,但是在满足 判断条件
x>0的前提下 ,操作x+1还是可以让x趋于正无穷
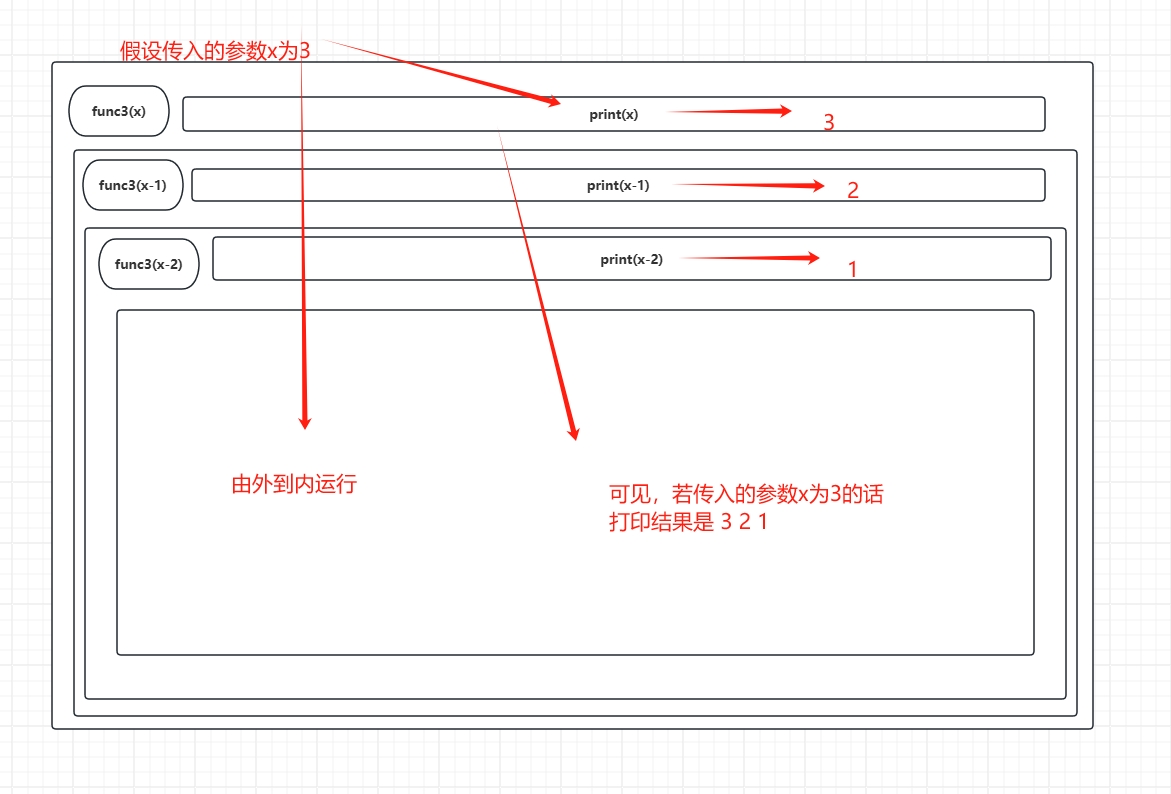
func3就可以算得上是一个递归函数了,因为有调用自身func3(x-1),也有结束条件
if x>0, 在这个条件语句下 ,操作 x -1 一直进行下去始终会达到 x< 0 的时候,那时候就是退出递归的时候...
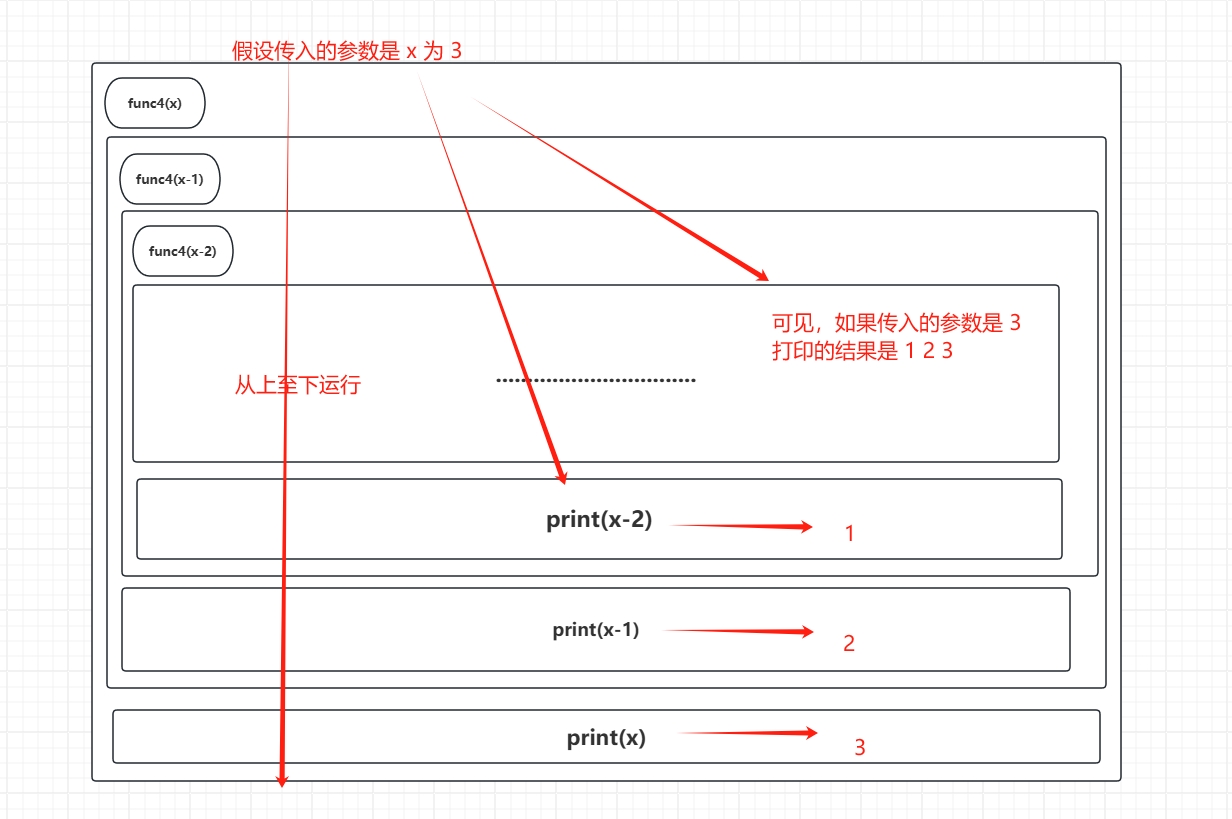
func4也是一个递归函数,因为有调用自身func4(x-1),也有结束条件
if x>0, 在这个条件语句下 ,操作 x -1 一直进行下去始终会达到 x< 0 的时候,那时候就是退出递归的时候...
❗
func3和func4区别 :对
func3画一个图描述它的运行可以是 :对
func4画一个图描述它的运行可以是:
- 可以发现,打印和调用递归函数的顺序不一样,产生的结果也不一样 !
1_1、汉诺塔问题

大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上
从下往上按照大小顺序摞着64片黄金圆盘。
大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。
在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
64 片黄金圆盘移动完毕之日,就是世界毁灭之时
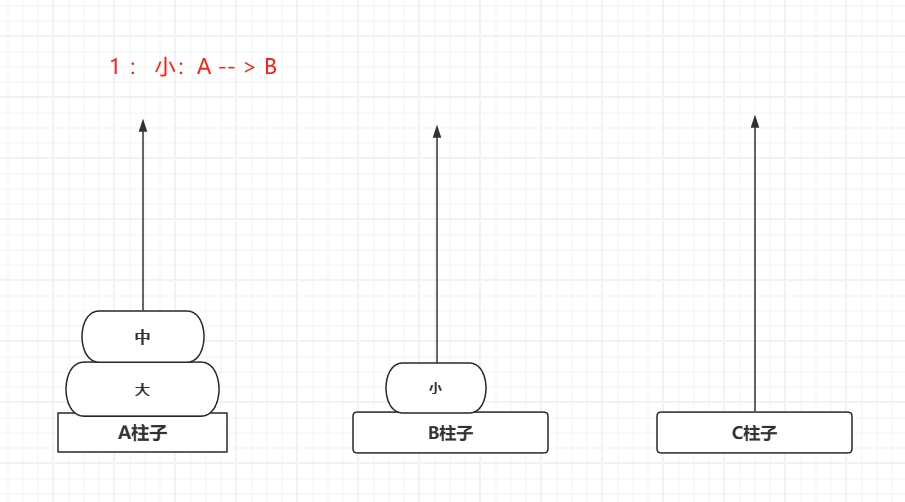
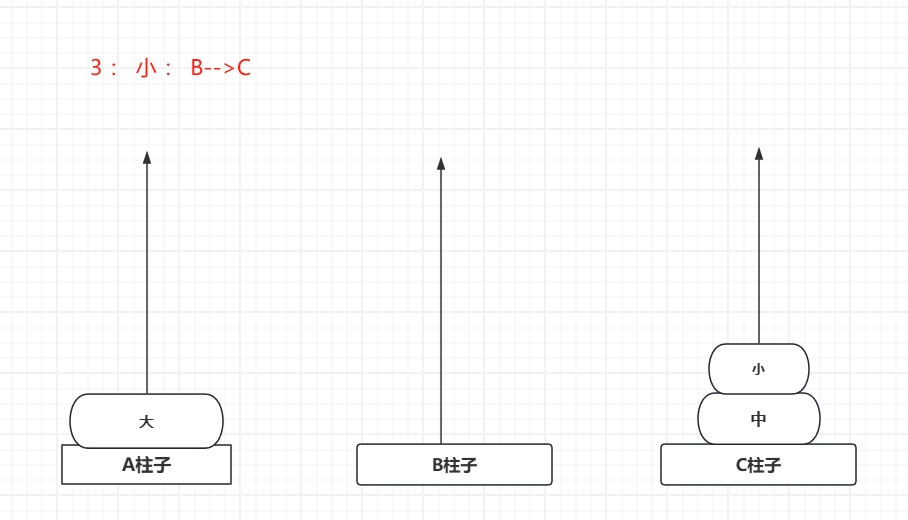
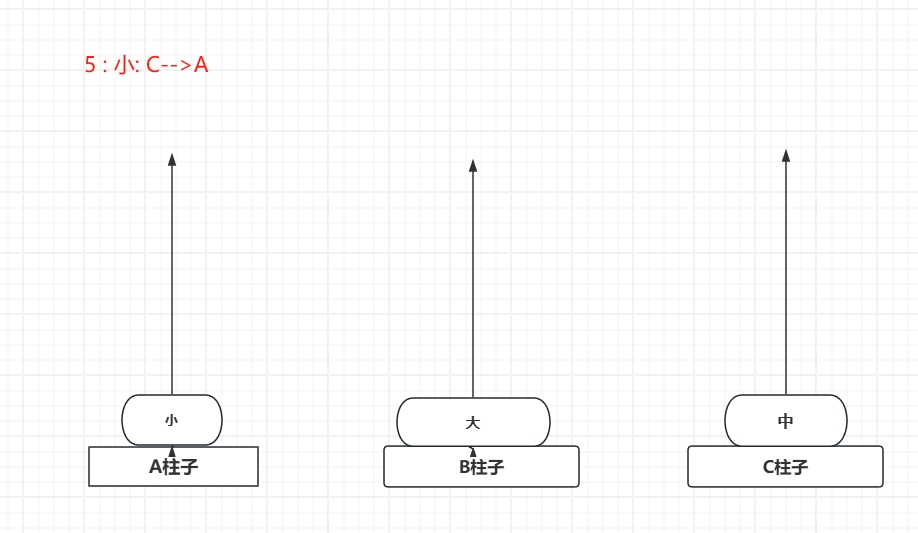
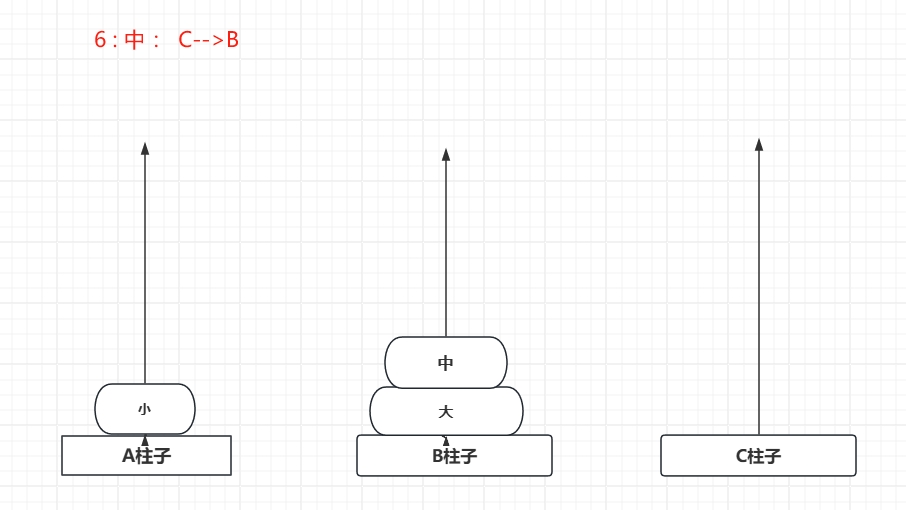
下面演示一下三个圆盘的移动情况:
可见,要在规则内 (小圆盘必须在大圆盘上面)把 A 上面 3 片移动到B 也用了 7步...
分析一下递归实现思路:
- 当需要把n个盘子从A经过B移动到C:
- Step1:把 n-1 个圆盘 从A经过C移动到B
- Step2:把 第n个圆盘 从A移动到C
- Step3:把 n-1 个圆盘 从B经过A移动到C
三个步骤,可以发现只有第二个步骤是一个( 原子操作 ),也就是最小的一个操作,不可再细分的
而步骤一和步骤三都只是把问题进行了简化...
我们就可以用这种递归思路来不断简化问题,直到都变成原子操作为止...
接下来尝试一下用 Python代码实现一下这个步骤:
python# 汉诺塔问题 def hanoi(n, a, b, c): """ 把n个盘子,从a柱子,利用b柱子,移动到c柱子上 :param n: 有几个盘子 :param a: n个盘子一开始在哪个柱子上 :param b: n个盘子可以利用哪根柱子去到目标柱子上 :param c: n个盘子需要移动到的目标柱子 :return: """ if n > 0: # Step1:把 n-1 个圆盘 从A经过C移动到B hanoi(n - 1, a, c, b) # Step2:把 第n个圆盘 从A移动到C print("moving from %s to %s" % (a, c)) # Step3:把 n-1 个圆盘 从B经过A移动到C hanoi(n - 1, b, a, c) hanoi(3,'A','B','C')运行结果:
textmoving from A to C moving from A to B moving from C to B moving from A to C moving from B to A moving from B to C moving from A to C
那么回到问题背景:
关于
“64 片黄金圆盘移动完毕之日,就是世界毁灭之时”我们可以做一下64次的讨论:
- 汉诺塔移动次数的递推式子:
h(x) = 2h(x-1)+1- h(64) = 18446744073709551615
- 假设婆罗门每秒钟搬一个盘子,则总共需要
5800亿年!!!
二、贪心算法
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在 。
也就是说,不从整体最优上加以考虑,它所做出的是在某种意义上的 。
贪心算法 并不保证会得到最优解,但是在某些问题上贪心算法的解就是最优解。
要会判断一个问题能否用贪心算法来计算。
2_1、找零问题
题目 : 假设商店老板需要找零 n 元钱 ,钱币的面额有 : 100元、50元、
20元、5元、1元,如何找零使得所需钱币的数量最少?
分析: 如 上面贪心算法的描述所说:
- 贪心算法在对问题求解时总是做出在 。
那么在这个问题背景,要求的是
钱币数量最少在这个要求背后,面额越大的钱币,那么数量就会越少
所以
代码实现:
pythont = [100, 50, 20, 5, 1] # 有的钱币面额 def change(t, n): """ 传入一共有哪些钱币面额的列表 t 还有需要找零多少钱 n 返回 m 对应每个钱币的数量的列表,还需要找零的钱数 n :param t: 钱币面额列表 :param n: 需要找多少钱 :return: m 对应每个钱币的数量的列表,还需要找零的钱数 n """ # 每个钱币多少张数 m列表 ,初始化全为 0 m = [0 for _ in range(len(t))] for i, money in enumerate(t): m[i] = n // money # // 是整除 n = n % money # 更新还需要找零的钱数 return m,n print(change(t,376))运行结果:
text([3, 1, 1, 1, 1], 0)
- 即 3张100 , 1张50 , 1张20 , 1张5 ,1张1。还需要找零 0
2_2 、背包问题
一个小偷在某个商店发现有 n 个商品,第 i 个商品价值 vi 元 ,重 wi 千克。 他希望 ,但他的背包最多只能 容纳 W 千克 的东西。他应该拿走哪些商品?
0 - 1 背包: 对于一个商品,小偷要么把它完整拿走,要么留下。不能只拿走一部分,或把一个商品拿走多次。(商品为金条)
分数背包: 对于一个商品 , 小偷可以拿走其中任意一部分。(商品为金砂)
举例 :
- 商品1 : v1 = 60 , w1 = 10
- 商品2: v2 = 100, w2 = 20
- 商品3 :v3 = 120, w3 = 30
- 背包容量:W = 50
- ❓思考 : 对于
0 - 1 背包和分数背包,贪心算法是否都能得到最优解?为什么?
分数背包代码实现:
python# 每个商品元组表示(价格,重量) goods = [(60, 10), (100, 20), (120, 30)] # 商品按照单位重量价格来进行降序排序 goods.sort(key=lambda x: x[0] / x[1], reverse=True) def fractional_backpack(goods, w): """ 传入商品列表 goods,列表每一个元素是(价格,重量), 和背包最大可承受重量w,求出最大价值的取商品方法 :param goods: 传入商品列表 :param w: 传入背包最大可以承受的重量 :return: 最大价值total_v, 背包剩余重量m """ # m 记录每种商品取的比例,范围0-1 # 即0是不取,1是全取,(0,1)的分数就是取部分 m = [0 for _ in range(len(goods))] total_v = 0 # 记录取到的最大价值 for i, (price, weight) in enumerate(goods): if w >= weight: # 书包剩余可承担重量m 是可以完全装下本次遍历到的商品的全部重量weight的 m[i] = 1 # 1就是这个商品全取 total_v += price # 记录价值 w -= weight # 更新背包剩余可承受重量 else: # 这个分支就是 w < weight # 也就是 当前遍历到的商品的全部重量weight已经大于可承受重量了,不能全部取,只能取一部分(分数) m[i] = w / weight # 注意,当前weight大于w,weight在分母这种算法得到的才是小于1的分数 total_v += m[i] * price # 记录价格 w = 0 # 背包取满了,没有可剩余重量 return total_v, m print(fractional_backpack(goods,50))
2_3、拼接最大数字问题
有 n 个 非负整数,将其按照字符串拼接的方式拼接为一个整数。
如何拼接可以使得得到的整数最大?
例:32,94,128,1286,6,71 可以拼接的最大整数为 94716321286128
分析 :
像刚刚那个例子,一共 6 个 非负整数 ,我们可以穷举出所有情况,然后取最大的那个
那么上面那6个数,按照位置顺序不一样来 “ 排队 ” 就是一共有 A66,也就是6的阶乘,一共720种情况
这才只有 6 个 !!! 显然这种方式在 n 变大后,时间花销将非常大!!
那么我们应该想一种更好的算法来让他们 “ 排队 ” 。
要是学过冒泡排序的话,那种思想我们可以借鉴一下
回忆一下:冒泡排序(升序)是比较两个相邻的数,数字大的往后排,然后不断比较相邻的
那么如果是降序的话同理 ,不断比较两个相邻的数,数字小的往后排...
那么我们可以设计一种比较方式,使得相邻的两个数拼接起来得到的数最大为标准
例:
如果对于相邻的两个数是 128 和 1286
那么他们可以拼接成 1281286 和 1286128
显然 1286128 > 1281286
那么我们就可以像下面一样书写代码
pythona = '128' b = '1286' a + b if a + b > b + a else b + a
ps :
这里的加号是字符串拼接,不是数学运算
因为 a + b 和 b + a 拼接出来的字符串是长度相同的,那么大于符号就会按照从前向后对比数字,
像 1286128 和 1281286 的第 4 个位置,前者是6,后者是1,那么前面就大于后面
如果我们写好比较规则,然后按照这个规则排好序,然后再拼接起来不就是最大的数字了吗!
自定义比较规则然后排序,在python2的sort里有个cmp参数,但现在python3没有了
在python3我们可以
from functools import cmp_to_key来写自定义cmp代码实现:
pythonfrom functools import cmp_to_key li = [32,94,128,1286,6,71] def xy_cmp(x,y): """ x和y是两个相邻的元素 :param x: 位于左边的元素 :param y: 位于右边的元素 :return: return 1 意思是 x 大于 y return -1 意思是 x 小于 y return 0 意思是 x 与 y 相等 """ # sort如果不传参reverse,默认是升序排序 # 那么 return 1 意思是 x 大于 y # 也就说明 x 需要往后走,才能构成升序排序,所以需要交换xy位置 if x+y < y+x: return 1 # 默认升序排序,return -1 意思是 y 大于 x # 那么 x 在 y 的前面这个顺序本来就是对的,所以不用交换xy位置 elif x+y > y+x: return -1 # return 0 就是 xy 是相等的,不用交换位置 else: # x+y == y+x return 0 def number_join(li): li = list(map(str,li)) li.sort(key = cmp_to_key(xy_cmp)) return "".join(li) print(number_join(li))运行结果:
text94716321286128
2_4、活动选择问题
假设有 n 个活动,这些活动要占用同一片场地,而场地在某时刻只能供一个活动使用。
每个活动都有一个
开始时间 si和结束时间 fi(题目中时间以整数表示),表示活动在
[ si , fi )区间占用场地。问:安排哪些活动能够使该场地 举办的活动的个数最多 ?
分析:
贪心结论 :
证明:假设 a 是所有活动中最先结束的活动,b是最优解中最先结束的活动。
如果 a = b , 结论成立 。
如果 a ≠ b , 则 b 的 结束时间一定晚于 a 的结束时间,则此时用 a 替换掉最优解中
的 b ,a 一定不与最优解中的其他活动时间重叠,因此替换后的解也是最优解。
代码实现:
python# 活动选择问题 # 活动用一个列表存储,每一个活动以 (开始时间,结束时间) 的形式表示 activities = [(1, 4), (3, 5), (0, 6), (5, 7), (3, 9), (5, 9), (6, 10), (8, 11), (8, 12), (2, 14), (12, 16)] # 保证活动是按照结束时间排好序的 activities.sort(key=lambda x: x[1]) def activity_selection(a): res = [a[0]] # 排序好的第一个就是结束时间最早的,先进入res列表 # 接下来遍历后续元素,查看与前面的时间有没有冲突,没冲突就进入res for i in range(1, len(a)): # 当前活动的开始时间大于等于最后一个入选活动的结束时间 if a[i][0] >= res[-1][1]: # 不冲突 res.append(a[i]) return res print(activity_selection(activities))运行结果:
text[(1, 4), (5, 7), (8, 11), (12, 16)]
三、迷宫问题
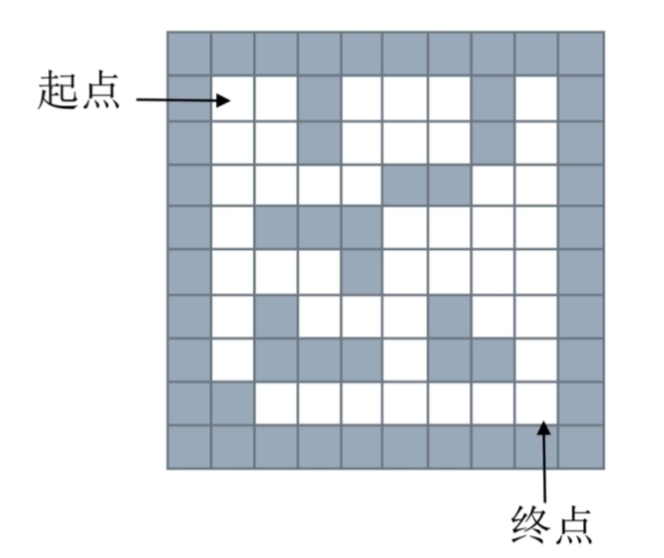
- 给一个二维列表,表示迷宫(0表示通道,1表示围墙)。给出算法,求一条走出迷宫的路径。

栈--深度优先搜索
回溯法
思路:从一个节点开始,任意找下一个能走的点,当找不到能走的点时,
退回上一个点寻找是否有其他方向的点。
使用栈存储当前路径
找到的是一条可行的路径,不一定是最短路径!
分析:
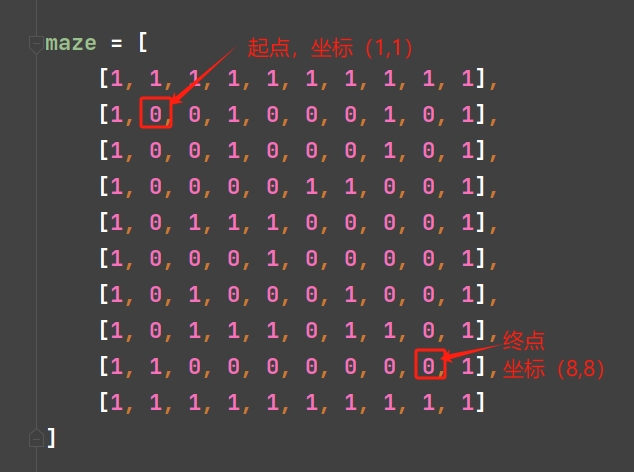
- 示例迷宫 :
textmaze = [ [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 0, 0, 1, 0, 0, 0, 1, 0, 1], [1, 0, 0, 1, 0, 0, 0, 1, 0, 1], [1, 0, 0, 0, 0, 1, 1, 0, 0, 1], [1, 0, 1, 1, 1, 0, 0, 0, 0, 1], [1, 0, 0, 0, 1, 0, 0, 0, 0, 1], [1, 0, 1, 0, 0, 0, 1, 0, 0, 1], [1, 0, 1, 1, 1, 0, 1, 1, 0, 1], [1, 1, 0, 0, 0, 0, 0, 0, 0, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1] ]
- 起点终点说明:
💡思路重新梳理:
从起点(1,1)开始,一个一个方向看,看哪个方向可以走(下一个点为0即可以走)
只要找到一个可以走的方向就先走,不管这个路后续能不能走
在代码中,
1表示迷宫的围墙 ,0表示可以走的路,且还没走过 ,2表示可以走的路,但是前面已经走到过了,即在遍历四个方向的时候,我们是不走1和2的,围墙和已经走过的路都视为不可走。当遇到四个方向,要不就是
1, 要不就是2, 说明这个路径已经走不通了,需要回溯到前面的点回溯的方法使用出栈,一开始栈内只有我们的起点(1,1),起点就是栈顶,越往后走的话,路径上的点都被记录到栈内,并且当前点就是栈顶的点,如果当前的点不可走了,要先记得把当前点重新赋值为
2, 表示这条路已经走过了,走不通了,后面就不会往这边走。然后搜索前面的点的其他可走的方向,要是前一个点也没了,就同样的操作出栈,然后就看再前一个点,后续同理...要是一直出栈,(因为我们知道,起点是一直保留在栈底的),直到起点也出栈了,那么栈就空了,换成代码来表示就是说
len(stack)<0, 这样就说明已经全部遍历过了都找不到一个可行的路径,换言之这个迷宫找不到一条可以通往终点的可行路线。我们可以用下面结构来在代码内表示:
while(len(stack)>0): ... ... else: print("没有路") return False四个方向可以用一个dirs 映射列表来实现,我们先思考好,位置在代码里是坐标表示,
那么四个方向的移动,是坐标的怎么样的变化??
# x,y 的四个方向 # 上:x-1,y # 下:x+1,y # 左:x,y-1 # 右:x,y+1那么我们就可以如下写一个dirs的映射列表:
# 写出四个方向的映射坐标 dirs = [ # 上 lambda x, y: (x - 1, y), # 下 lambda x, y: (x + 1, y), # 左 lambda x, y: (x, y - 1), # 右 lambda x, y: (x, y + 1) ]使用 dirs 的方式可以用下面的伪代码来理解:
cur_node = stack[-1] # 当前的节点 ... for dir in dirs: next_node = dir(cur_node[0], cur_node[1]) # 下一个节点 # 如果下一个节点能走(下个节点为0) if maze[next_node[0]][next_node[1]] == 0: ...
代码实现:
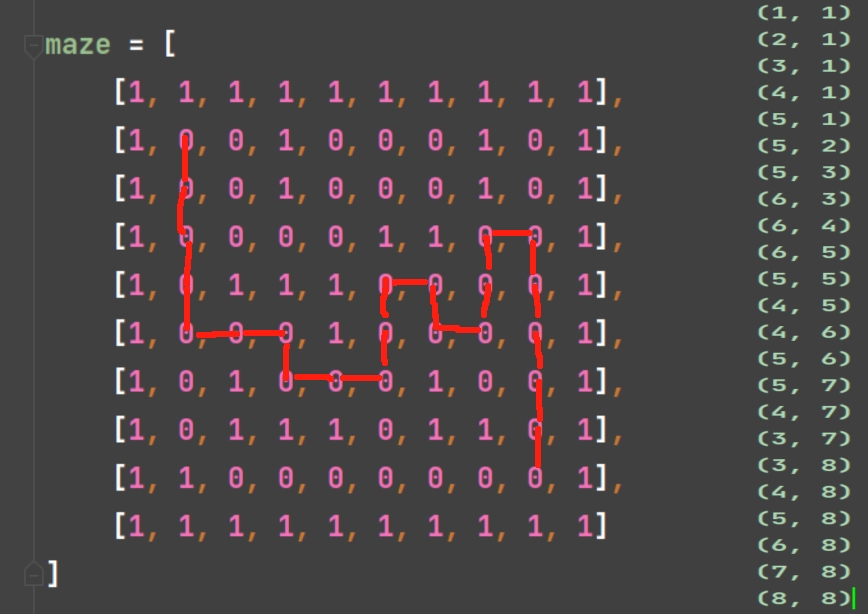
python# 栈的迷宫问题 # 深度优先算法 maze = [ [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 0, 0, 1, 0, 0, 0, 1, 0, 1], [1, 0, 0, 1, 0, 0, 0, 1, 0, 1], [1, 0, 0, 0, 0, 1, 1, 0, 0, 1], [1, 0, 1, 1, 1, 0, 0, 0, 0, 1], [1, 0, 0, 0, 1, 0, 0, 0, 0, 1], [1, 0, 1, 0, 0, 0, 1, 0, 0, 1], [1, 0, 1, 1, 1, 0, 1, 1, 0, 1], [1, 1, 0, 0, 0, 0, 0, 0, 0, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1] ] # 写出四个方向的映射坐标 dirs = [ # 上 lambda x, y: (x - 1, y), # 下 lambda x, y: (x + 1, y), # 左 lambda x, y: (x, y - 1), # 右 lambda x, y: (x, y + 1) ] def maze_path(x1, y1, x2, y2): """ :param x1: 起点横坐标 :param y1: 起点纵坐标 :param x2: 终点横坐标 :param y2: 终点纵坐标 :return: """ stack = [] # 存走过的路线 stack.append((x1, y1)) # 存入起点坐标 maze[x1][y1] = 2 # 初始化节点为已经走过 while (len(stack) > 0): # 当栈还不空就一直循环 # 因为回溯是往回找,不能走的点就会pop出栈,还有点在栈内就可以一直往回回溯 cur_node = stack[-1] # 当前的节点 if cur_node[0] == x2 and cur_node[1] == y2: # 如果当前的节点横纵坐标与终点横纵坐标对应,说明走到终点了 # 那么当前的stack里面就是一个可行的路线(可能不是最短路径) # 遍历stack,打印出路线经过的坐标点 for p in stack: print(p) return True # x,y 的四个方向 # 上:x-1,y # 下:x+1,y # 左:x,y-1 # 右:x,y+1 global next_node # for-else结构,global使得else可以与for里面的局部变量定义联系起来 for dir in dirs: # 把当前节点的横纵坐标传入遍历出来的dir四个方向 # 得出四个方向的下一个节点,如果下一个节点是0就是可走的方向 # 由于是深度优先遍历,所以按照遍历顺序找到一个方向可走就可以不用继续遍历了 # 假如这个方向后续是走不通的再回溯 next_node = dir(cur_node[0], cur_node[1]) # 下一个节点 # 如果下一个节点能走(下个节点为0) if maze[next_node[0]][next_node[1]] == 0: stack.append(next_node) # 可走的下一个节点入栈 maze[next_node[0]][next_node[1]] = 2 # 2 表示节点标记为已走过 break # 找到能走就可以退出了 # 如果上面的for循环正常退出(即没通过break退出)(即没找到一个可行的方向) # 说明进入else是不可走了,需要回溯了 else: maze[next_node[0]][next_node[1]] = 2 # 走过,且为不可行路线,标记为2 stack.pop() # 然后回溯 else: print("没有路") return False # maze_path函数调用 maze_path(1,1,8,8)运行结果:
python(1, 1) (2, 1) (3, 1) (4, 1) (5, 1) (5, 2) (5, 3) (6, 3) (6, 4) (6, 5) (5, 5) (4, 5) (4, 6) (5, 6) (5, 7) (4, 7) (3, 7) (3, 8) (4, 8) (5, 8) (6, 8) (7, 8) (8, 8)按照这个结果,我们可以试着看看它搜索的路线是怎么样的:
不得不说,在我们拥有全局视野的前提下,这个搜索路线走得好像有点太傻了~(可能是我故意为之)
但这种搜索,在我们不需要最短路径的时候,一般又都是可以使用这种处理方式
因为它不需要特别庞大的存储空间,就反复地出栈入栈
就起码可以帮助我们找到一条可行的路线...
队列--广度优先搜索
- 思路:从一个节点开始,寻找所有接下来能继续走的点,继续不断寻找,直到找到出口。
- 使用队列存储当前正在考虑的节点。
- 可以找到最短路径!
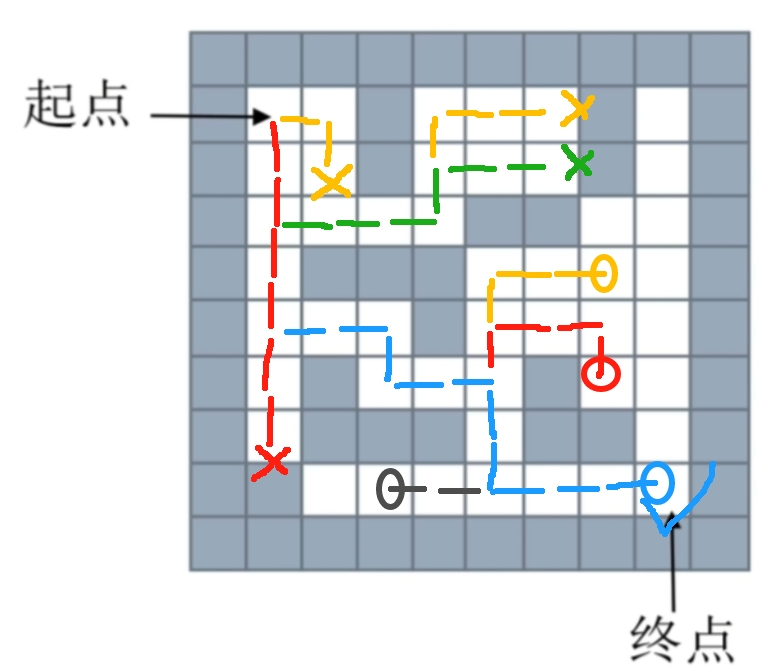
- 图示思路:
上图解释:
方向的优先级是:下 > 右 > 上 > 左
每一个路径都同时走一步,用不同颜色来标识不同路径
因为是同时走一步,最先走到终点的就是步数最少的,即最短路径
补充:这跟水蔓延找迷宫出口一个道理,在起点倒水,水是以同样速度向不同方向蔓延的,
先到终点的那批水所经过的路线就是最短的。
💡思路重新梳理:
代码内队列将调用内置库
collections里面的双端队列的类deque。首先依旧是把起点(1,1)加入到队列里面,但与栈的迷宫问题不同的是,这里不止传入节点的横纵坐标,还有第三个值表示上一个点的信息,由于是起点,无前一个点的信息,第三个值设为-1(表示无前一个点),且为路径终止条件。对应代码
queue.append((x1, y1, -1))。还有更大的区别是:队列迷宫问题中的队列只存储每一条路径上当前的最后一个点。用队列的原因也很简单,让这些 “ 最后一个点 ” 依次排好队,轮流去遍历四个方向,这样可以保证不同方向,不同路径的行走速度都是相同的,从而保证最先到达终点的点走过的路径就是最短路径!
由于第三点的这个原因,那我们虽然有一个最快到达终点的点,但没有存储路径信息啊,我们怎么输出那个最短路径呢??那么就需要用到额外的一个
path列表来存储通过的节点坐标和该节点坐标的前驱节点坐标的信息了,有这个列表我们就可以使用到达终点的那个点的前驱节点信息一个一个往前找,找到起点为止,这个找的过程一个一个添加到一个新的列表里,然后把这个列表逆序输出就是最短路径信息!!
关于第四点的描述,我们可以定义一个函数来实现,函数参数就是传入构建好的
path:def print_r(path): # 下面找到终点了才会调用print_r,那么path的最后一个值,path[-1]就是终点参数 # 利用终点参数的第三个值,还有path列表逐步往回找到最短路径 cur_node = path[-1] realpath = [] # 存储最短路径 while cur_node[2] != -1: # 前面我们把起点的第三个值设为了-1 # 当没有找到起点,就一直循环 realpath.append(cur_node[0:2]) # 路径只记录坐标就好,不需要第三个值了 cur_node = path[cur_node[2]] # 找前一个点 realpath.append(cur_node[0:2]) # 最后添加上起点 realpath.reverse() # 逆序之后就是最短路径 for node in realpath: print(node)有一个关键点需要注意:在栈的迷宫问题里,我们遍历四个方向去找可以走的方向的时候的代码是:
pythoncur_node = stack[-1] # 当前的节点 ... for dir in dirs: next_node = dir(cur_node[0], cur_node[1]) # 下一个节点 # 如果下一个节点能走(下个节点为0) if maze[next_node[0]][next_node[1]] == 0: ... break # !!!!!!!!!!!! 栈是找到一个可以走的点就退出的队列的迷宫问题里我们是每个方向都找,且都进入队列的 !!
代码实现:
python# 队列实现迷宫问题 # 广度优先算法 from collections import deque # 导入deque maze = [ [1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 0, 0, 1, 0, 0, 0, 1, 0, 1], [1, 0, 0, 1, 0, 0, 0, 1, 0, 1], [1, 0, 0, 0, 0, 1, 1, 0, 0, 1], [1, 0, 1, 1, 1, 0, 0, 0, 0, 1], [1, 0, 0, 0, 1, 0, 0, 0, 0, 1], [1, 0, 1, 0, 0, 0, 1, 0, 0, 1], [1, 0, 1, 1, 1, 0, 1, 1, 0, 1], [1, 1, 0, 0, 0, 0, 0, 0, 0, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1] ] # 写出四个方向的映射坐标 dirs = [ # 下 lambda x, y: (x + 1, y), # 上 lambda x, y: (x - 1, y), # 左 lambda x, y: (x, y - 1), # 右 lambda x, y: (x, y + 1) ] def print_r(path): # 下面找到终点了才会调用print_r,那么path的最后一个值,path[-1]就是终点参数 # 利用终点参数的第三个值,还有path列表逐步往回找到最短路径 cur_node = path[-1] realpath = [] # 存储最短路径 while cur_node[2] != -1: # 前面我们把起点的第三个值设为了-1 # 当没有找到起点,就一直循环 realpath.append(cur_node[0:2]) # 路径只记录坐标就好,不需要第三个值了 cur_node = path[cur_node[2]] # 找前一个点 realpath.append(cur_node[0:2]) # 最后添加上起点 realpath.reverse() # 逆序之后就是最短路径 for node in realpath: print(node) def maze_path_queue(x1, y1, x2, y2): """ :param x1: 起点横坐标 :param y1: 起点纵坐标 :param x2: 终点横坐标 :param y2: 终点纵坐标 :return: """ queue = deque() # 与栈的迷宫问题实现区别,这里不止传入节点的横纵坐标,还有第三个值表示上一个点的信息 # 传入起点值,且无前一个点的信息,第三个值设为-1(表示无前一个点),且为路径终止条件 queue.append((x1, y1, -1)) # 标记为已经走过 maze[x1][y1] = 2 # queue记录每一条路径可行的最后一个节点,path记录走过的节点,以便后面找到最短路径 # path里面的每一个元素的结构是 (坐标点的横坐标,坐标点的纵坐标,这个坐标点在迷宫里的前一个点在path所对应的索引) path = [] while len(queue) > 0: # 与栈的迷宫问题不同,队列的迷宫问题在遍历当前节点的时候 # 就把队列里对应的这个节点给pop()掉了 # 因为队列迷宫问题中的queue只存储每一条路径的最后一个坐标点的参数 # 用极限一点的情况来说,假如起点的四个方向都是墙,也就是起点就无法找到可行方向 # 那么这个cur_node赋值后,同时queue里pop掉起点后 # 那么找不到方向就会没有next_node进入队列,那么queue就还是空的 # 在queue还是空的情况下跳出本次循环 # 那么下次循环条件 len(queue)>0 就不满足 cur_node = queue.popleft() path.append(cur_node) # 如果当前的节点横纵坐标与终点横纵坐标对应,说明走到终点了 if cur_node[0] == x2 and cur_node[1] == y2: # 走到终点了 # 打印最短路径 print_r(path) return True # 遍历四个方向,找可走的方向 for dir in dirs: # 把当前节点的横纵坐标传入遍历出来的dir四个方向 # 得出四个方向的下一个节点,如果下一个节点是0就是可走的方向 next_node = dir(cur_node[0], cur_node[1]) # 下一个节点 # 下一个节点是0就可走 if maze[next_node[0]][next_node[1]] == 0: # 后续节点进队,记录是哪个节点带他来的 # 假如现在是起点第一次遍历到这,那么cur_node就是起点 # 起点cur_node现在在path里面,那么len(path)-1也就是等于1-1等于0(起点cur_node在path中的下标) # 可见,这样可以记录每一次找到新结点时,前一个节点在path里面的下标作为第三个值 queue.append((next_node[0], next_node[1], len(path) - 1)) maze[next_node[0]][next_node[1]] = 2 # 标记为已走过 """ !!!这个位置注意: 与栈的迷宫问题不同,栈的迷宫问题找到一个可以走的方向就break了, 但是队列的迷宫问题会把所有可以走的方向都加入到队列里面, 每一条道路都《同时走一步》 遍历 那么最先走到终点的那个道路,就是最短的路径 """ else: # while循环的else,也就是说队列为空了还没有return,即没找到可行的路 print("没有路") return False maze_path_queue(1,1,8,8)运行结果:
text(1, 1) (2, 1) (3, 1) (4, 1) (5, 1) (5, 2) (5, 3) (6, 3) (6, 4) (6, 5) (7, 5) (8, 5) (8, 6) (8, 7) (8, 8)按照这个结果,我们可以试着看看它搜索的路线是怎么样的:
比起前面那个深度优先搜索的路线,这个简直就是 “显而易见” 的最短路径啊!!
💡 即兴
一、牛顿-牛吃草问题
牛吃草问题 - v1
一堆草,可供 10 头牛吃 3 天 ,那可供 6 头牛吃几天?
3 × 10 ÷ 6 = 5 天
牛顿 - 牛吃草问题
英国著名的物理学家牛顿曾把题目变成了这样:
- 牧场上有一片青草,每天都生长得一样快。这片青草供给24头牛吃,可以吃6天,或者供给20头牛吃,可以吃10天,期间一直有草生长。如果供给19头牛吃,可以吃多少天?
这道题因牛顿提出而得名 “ 牛顿问题 ”
- 牛每天都在吃草,草每天在不断均匀生长
- 解题环节主要有三步
- 求出每天长草量
- 求出牧场原有草量
- 求出牛可吃天数
设一头牛一天吃的草为一份
24 头牛 6 天吃草为 1×24×6=144份,20头牛10天吃草 1×20×10=200份
无论是144还是200都是吃净了草地的原有草量和每日的新增草量
- 原有草量 + 每天生长草量 × 6 = 144 份
- 原有草量 + 每天生长草量 × 10 = 200 份
所以 下式减上式:(200-144) = 每天生长草量 × 10 - 每天生长草量 × 6
所以:
- 56 = 每天生长草量 × 4
说明牧场每天生成草量为 14 份
- 原有草量 + 每天生长草量(14份)× 6 = 144 份
所以 144 - 14 × 6 = 原有草量,说明原有草量为 60 份
问题转述:原有草量为60份,每天生长草量为14份,那么够19头牛吃几天
pythonx = 1 # x 记录天数 while True: if 60 + 14 * x == 19 * x * 1: break else: x += 1 print(x)运行结果:
text12
牛顿问题中还有一些变形题目,比如:
- 冬天时牧场的草不是每天增长而是会每天的减少,问这种情况下可以供N头牛吃多少天?
- 牧场的草每天都在增长,可供牛吃N天,问有多少头牛?
- 抽水问题
- 滚梯行走问题
- 售票窗口问题
二、字符和ASCII转换
2_1、chr()
chr(i):这是一个将 的字符的函数。i是一个介于 0 到 127 之间的整数(在 Python 3 中可以是 0 到 1114111,对应于 Unicode 码点),chr(i)会返回对应的字符。
示例代码:
pythonprint(chr(65)) # A
2_2、ord()
ord(c):这是一个 (在 Python 3 中是 Unicode 码点)的函数。c是一个单个字符,ord(c)会返回对应的整数。
示例代码:
pythonprint(ord('A')) # 65
注意:
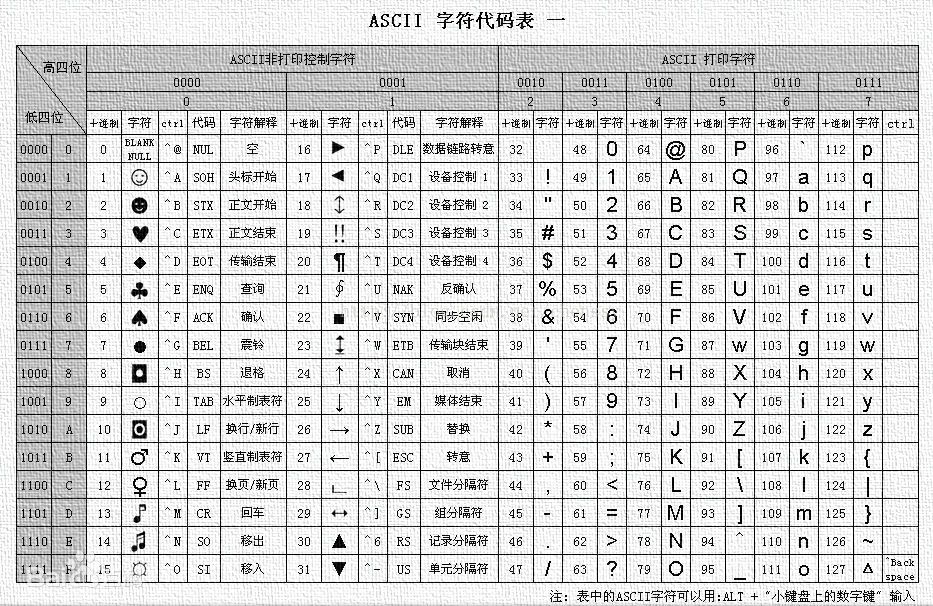
ASCII码表如下:
在
ASCII中 , 可以注意到 A 是 65 ,然后 对应的小写字母 a 是 97 ,相差 97 - 65 = 32这个规律在其他字母也同理,也就是字母的小写字母对应的 ascii码值
总是比它对应的大写字母的 ascii码值 大32
例题( 洛谷P2433问题12 ):
- 大家都知道有 26 个英文字母,其中 A 是第一个字母。现在请编程求出:
- M 是字母表中的第几个字母?
- 第 18 个字母是什么?
- 输出一个数字和一个字母,使用换行隔开。
python# 比如 B 是字母表第二个字母,那么ord('B') - ord('A')得到的是 1 # 所以说要获取 B在字母表的位置为ord('B') - ord('A') +1 # 同理 M位置要写成 ord('M') - ord('A') + 1 print(ord('M') - ord('A') + 1) # A是字母表第一个位置的 # 如果要获取第二个位置,就是chr(ord('A') + 1)就能得到 B # 所以第18个位置 chr(ord('A') + 17) print(chr(ord('A') + 17))运行结果:
text13 R
三、f - string 的高级用法
Python 的字符串格式化方法
f-string提供了一种非常灵活的方式来格式化字符串。以下是一些
f-string的高级用法 :
1.指定宽度和填充字符
{:10d}: 将整数格式化为至少 10个字符宽,如果不足10位则用空格填充。{:>10d}:使用右对齐,不足部分用空格填充。{:<10d}:使用左对齐,不足部分用空格填充。{:^10d}:使用居中对齐,不足部分用空格填充。{:*^10d}:使用*字符填充,居中对齐。示例代码:
pythoncontrast = 1000000000 # 10位整数 text = 2024 # 4位整数 print(contrast) print(f"{text:10d}") # 宽度设为10,默认右对齐 print(f"{text:>10d}") # 右对齐 print(f"{text:<10d}") # 左对齐 print(f"{text:^10d}") # 居中对齐 print(f"{text:*^10d}") # 使用*字符填充,居中对齐运行结果:
text1000000000 2024 2024 2024 2024 ***2024***
2.指定精度
{:.2f}:浮点数格式化为保留两位小数。{:.6g}:浮点数格式化为保留6位有效数字。示例代码:
pythonfrom math import pi print(pi) print(f"{pi:.2f}") print(f"{pi:.6g}")运行结果:
python3.141592653589793 3.14 3.14159
3.使用千分位分隔符
{:,}:整数格式化为千分位分隔。示例代码:
pythona = 123456789.123456 print(f"{a:,}")运行结果:
text123,456,789.123456
4.零填充
{:05d}:整数格式化为至少5个字符宽,不足部分用0填充。示例代码:
pythontext = 2024 print(f"{text:010d}") # 10个宽度,不足用0填充运行结果:
text0000002024
5.百分比格式化
{:.2%}:浮点数格式化为百分比形式,保留两位小数。示例代码:
pythona = 0.56789 print(f"{a:.2%}")运行结果:
text56.79%
6.科学计数法
{:e}:浮点数格式化为科学记数法(例如:1.23e+02)。{:.2e}:浮点数格式化为科学记数法,保留两位小数。示例代码:
pythona = 567890000.123456 print(f"{a:e}") print(f"{a:.2e}")运行结果:
text5.678900e+08 5.68e+08
7.十六进制格式化
{:x}:整数格式化为十六进制形式(小写字母)。
{:X}:整数格式化为十六进制形式(大写字母)。补充:
- 16进制有部分用字母代替 0-9 还是数字
- 10 - 15 为 a b c d e f
补充:可以使用内置函数
hex()转 十六进制
num = 255 print(hex(255)) # 0xff print(f"{num:x}") # ff # 使用hex()转换,前面会有 0x 标识这个数是十六进制的示例代码:
pythona = 15 b = 30 c = 16 print(f"{a:x}") # 整数第一位的最后一个 15 --> f print(f"{c:x}") # 整数第二位重新开始算 16 --> 10 print(f"{b:x}") # 小写 print(f"{b:X}") # 大写运行结果:
textf 10 1e 1E
8.二进制格式化
{:b}:整数格式化为二进制形式。补充:可以使用内置函数
bin()转二进制
num = 255 print(bin(num)) # 0b11111111 # 使用bin()转换,前面会有 0b 标识这个数是二进制的示例代码:
pythonnum = 255 sos = 6 print(f"{num:b}") print(f"{sos:b}")运行结果:
python11111111 110
9.八进制格式化
{:o}:整数格式化为八进制形式。- 补充: 可以使用内置函数
oct()转八进制示例代码:
pythonnum = 255 print(oct(num)) print(f"{num:o}") # 使用oct()转换,前面会有 0o 标识这个数是八进制的运行结果:
text0o377 377
10. 格式化字符串
{!s}:将对象格式化为字符串形式 (__str__)。{!r}:将对象格式化为可打印的字符串形式(__repr__)。不常用,先不做详细解释~~
11.条件表达式
{x if condition else y}:如果条件为真,则格式化为x,否则为y。示例代码:
pythontemperature = 20 message = f"Today's temperature is {temperature} degrees. It's {('hot' if temperature > 25 else 'not hot')} outside." print(message)运行结果:
textToday's temperature is 20 degrees. It's not hot outside.
12.嵌套格式化
{:>{width}}:可以嵌套使用,例如{:>{10}}表示右对齐,宽度为10。示例代码:
pythoncontrast = 1000000000 # 10位整数 text = 2024 # 4位整数 print(contrast) print(f"{text:{0}<{10}}") # 用0填充,左对齐,宽度为10运行结果:
text1000000000 2024000000
四、数学模块:math
1. 常量
math.pi:圆周率π的值。math.e:自然对数的底数e。pythonimport math print(math.pi) # 3.141592653589793 print(math.e) # 2.718281828459045
2. 幂函数
math.pow(x, y):计算x的y次幂,即x^y。math.sqrt(x):计算x的平方根。pythonimport math print(math.pow(2,3)) # 8.0 print(math.sqrt(9)) # 3.0
- 注意:
- 有时候我们知道
math.sqrt()是求平方根,然后当遇到要求一个立方根的时候就懵逼了...- 其实我们可以这样想,
math.pow(x,y)是求x的y次幂- 那么
math.sqrt(9)不也可以写成math.pow(9,1/2)这样吗,1/2次幂不就是开根号- 那么思路打开,求立方根不就是
math.pow(8,1/3)这样...
3. 对数函数
math.log(x[, base]):计算x的自然对数(以e为底)。如果指定了base,则计算以base为底的对数。
math.log2(x):计算x的以2为底的对数。
math.log10(x):计算x的以10为底的对数。pythonimport math print(math.log(math.e ** 10)) # 10.0 print(math.log(8,2)) # 3.0 print(math.log2(8)) # 3.0 print(math.log10(100)) # 2.0
4. 三角函数
math.sin(x):计算x的正弦值。x是以弧度为单位的角度。math.cos(x):计算x的余弦值。x是以弧度为单位的角度。math.tan(x):计算x的正切值。x是以弧度为单位的角度。math.asin(x):计算x的反正弦值,并返回弧度值。math.acos(x):计算x的反余弦值,并返回弧度值。math.atan(x):计算x的反正切值,并返回弧度值。math.atan2(y, x):计算y/x的反正切值,并考虑x的符号以确定正确的象限。pythonimport math pi = math.pi print(pi) # 3.141592653589793 print(math.sin(pi / 2)) # 1.0 print(math.cos(0)) # 1.0 print(math.tan(pi / 4)) # 0.9999999999999999 # 正是因为math里面的pi也不是完美的pi,所以代入计算会跟我们数学时有些许偏差
5. 双曲函数
math.exp(x):计算e的x次幂。math.hypot(x, y):计算直角三角形的斜边长度,其中x和y是直角边的长度。pythonimport math print(math.exp(2)) print(math.e ** 2) print(math.hypot(3,4))
- 补充:
math.hypot(x,y)也叫求欧几里得范数。- 欧几里得范数 就是从原点到点 (x,y) 的直线距离,即勾股定理所描述的直角三角形的斜边长度
- 即求 x与y的平方和开根号
6. 舍入函数
math.ceil(x):对x进行向上舍入到最近的整数。math.floor(x):对x进行向下舍入到最近的整数。math.fabs(x):计算x的绝对值。math.trunc(x):将x舍入到最近的整数,直接去掉小数部分。pythonimport math print(math.ceil(3.1)) # 4 print(math.floor(3.9)) # 3 print(math.fabs(-1.23)) # 1.23 print(math.trunc(3.1)) # 3 print(math.trunc(3.9)) # 3
7. 角度和弧度的转换
math.degrees(x):将弧度转换为角度。math.radians(x):将角度转换为弧度。pythonimport math print(math.degrees(math.pi)) # 180.0 print(math.radians(180)) # 3.141592653589793
8. 其他函数
math.gcd(a, b):计算两个整数a和b的最大公约数。math.factorial(x):计算x的阶乘,x必须是非负整数。math.fmod(x, y):计算x除以y的余数。math.modf(x):将x分解为整数部分和分数部分,返回一个元组。pythonimport math print(math.gcd(145,25)) # 5 print(math.factorial(5)) # 120 print(math.fmod(8, 5)) # 3.0 print(math.modf(3.5)) # (0.5, 3.0) # math.modf(x)还是不要用好,由于计算机使用二进制格式存储浮点数 # 某些十进制小数无法被精确表示为二进制形式,会出现误差
五、时间模块:time&datetime
- UTC / GMT : 世界时间
- 本地时间 : 本地时区的时间
Python中关于时间处理的模块有两个,分别是 time 和 datetime 。
5_1、time
获取当前时间戳 (自1970-1-1 00:00)pythonimport time # 获取当前时间戳 (自1970-1-1 00:00) v1 = time.time() print(v1)运行结果:
text1730784583.0720701
时区偏移量pythonimport time # 时区 # 用来表示当前时区相对于UTC(协调世界时)的偏移量,单位是秒 v2 = time.timezone # 位于东八区(北京时间),那么相对于UTC的偏移量是 -28800秒(即8小时) # 这里的负号表示本地时间(东八区)比UTC时间晚,或者说UTC时间比本地时间早。 print(v2/60/60) # /60/60 --> 获取小时偏移量运行结果:
text-8.0
time.sleep(n) 休眠,暂停运行n秒pythonimport time # time.sleep(n) 休眠,暂停运行n秒 start = time.time() # 记录一个开始的时间戳 print("...") # 模拟程序代码 time.sleep(3) # 休眠3秒 print("...") # 模拟程序代码 end = time.time() # 记录一个结束的时间戳 print(f"程序开始到结束用时:{end - start}")运行结果:
text... ... 程序开始到结束用时:3.0137882232666016这里占据程序绝大部分时间的3秒,就是我们设置的休眠的3秒
5_2、datetime
datetime 是一种特殊的数据类型,它不是字符串!
在平时开发过程中的时间一般是以如下三种格式存在:
datetimepythonfrom datetime import datetime,timezone,timedelta v1 = datetime.now() # 当前时间 print(v1) tz = timezone(timedelta(hours=7)) # 当前东7区时间 v2 = datetime.now(tz) # 可以发现与上面当前时间(北京时间)(东八区)刚好差一个小时 print(v2) v3 = datetime.utcnow() # 当前UTC时间 # UTC和上面东八区,东七区时间分别刚好相差8小时和7小时 print(v3)运行结果:
text2024-11-05 13:39:30.972360 2024-11-05 12:39:30.972360+07:00 2024-11-05 05:39:30.972360
timedelta实现时间的加减
pythonfrom datetime import datetime,timedelta v1 = datetime.now() # 当前时间 print(v1) # 时间的加减 v2 = v1 + timedelta(days=140,minutes=5) print(v2)运行结果:
text2024-11-05 13:42:40.474562 2025-03-25 13:47:40.474562除了上面那样指定,同理还可以:
days=, seconds=, microseconds=,
milliseconds=, minutes=, hours=, weeks=
两个datetime时间间隔
pythonfrom datetime import datetime, timedelta v1 = datetime.now() # 当前(北京)时间 print(v1) v2 = datetime.utcnow() # 当前UTC时间 print(v2) # datetime之间相减,计算间隔时间(不能相加) date = v1 - v2 print(f"day偏移量:{date.days} | 小时偏移量{date.seconds / 60 / 60} | 毫秒偏移量:{date.microseconds}")运行结果:
text2024-11-05 13:50:35.467890 2024-11-05 05:50:35.467890 day偏移量:0 | 小时偏移量8.0 | 毫秒偏移量:0
- 注意:
- datetime 类型 和 timedelta 类型 可以加减
- datetime 类型和 datetime 类型 只能进行减,除外还可以进行比较大小
- 字符串
pythonfrom datetime import datetime # strptime的全称是“string parse time”,即字符串解析时间 # 字符串格式时间 --> 转换为datetime格式时间 text = "2024-10-24" v1 = datetime.strptime(text,"%Y-%m-%d") # 传入字符串和其格式 print(v1) print(type(v1))运行结果:
text2024-10-24 00:00:00 <class 'datetime.datetime'>python# datetime格式 --> 转换为字符串格式 from datetime import datetime # strftime的全称是“string format time。用于将时间以特定格式输出 v1 = datetime.now() val = v1.strftime("%Y-%m-%d %H:%M:%S") # 传入要转换成的字符串格式 print(v1) print(val)运行结果:
text2024-11-05 18:24:13.970078 2024-11-05 18:24:13
- 时间戳
python# 时间戳格式 --> 转换datetime格式 import time from datetime import datetime ctime = time.time() # 获取时间戳 v1 = datetime.fromtimestamp(ctime) print(v1) print(type(v1))运行结果:
text2024-11-05 18:27:11.762924 <class 'datetime.datetime'>python# datetime格式 --> 转换为时间戳格式 from datetime import datetime v1 = datetime.now() val = v1.timestamp() print(val) print(type(val))运行结果:
text1730802570.468446 <class 'float'>
5_3、补充
datetime和timedelta还有很多有用的属性和方法提供我们调用
最起码先知道怎么构造一个
datetime对象 ,才可以调用相关属性方法
from datetime import datetime
"""
# 构造一个 datetime 对象
# datetime_object = datetime(year, month, day, hour=0, minute=0, second=0, microsecond=0, tzinfo=None, fold=0)
参数说明
year:年份(必须提供,范围通常是 [1, 9999])。
month:月份(必须提供,范围是 [1, 12])。
day:日期(必须提供,范围是 [1, 31],具体取决于月份和是否闰年)。
hour:小时(可选,默认为 0,范围是 [0, 23])。
minute:分钟(可选,默认为 0,范围是 [0, 59])。
second:秒(可选,默认为 0,范围是 [0, 59])。
microsecond:微秒(可选,默认为 0,范围是 [0, 999999])。
tzinfo:时区信息(可选,默认为 None,可以是一个 tzinfo 对象)。
fold:用于处理夏令时等情况(可选,默认为 0,值为 0 或 1)。
"""
# 1.构造一个具体的日期和时间
dt = datetime(2024, 10, 24, 14, 30, 15, 123456)
print("日期和时间:", dt)
# 2.构造一个日期,时间默认为午夜
dt = datetime(2024, 10, 24)
print("日期和时间:", dt)
# 3.创建一个 date 对象和一个 time 对象
d = date(2024, 3, 25)
t = time(14, 30, 15)
# 组合成一个 datetime 对象
dt = datetime.combine(d, t)
print("组合后的日期和时间:", dt)获取基本的属性
from datetime import datetime
# 获取当前日期和时间
now = datetime.now()
print("年:", now.year)
print("月:", now.month)
print("日:", now.day)
print("时:", now.hour)
print("分:", now.minute)
print("秒:", now.second)
print("微秒:", now.microsecond)from datetime import timedelta
# 创建一个 timedelta 对象
delta = timedelta(days=10, hours=5, minutes=30, seconds=15, microseconds=12345)
# 获取天数
print("天数:", delta.days)
# 获取秒数
print("秒数:", delta.seconds)
# 获取微秒
print("微秒:", delta.microseconds)
# 获取总秒数
print("总秒数:", delta.total_seconds())某个
datatime对象的日期在它那周是属于第几天?
# weekday()
from datetime import datetime
# 获取当前日期
today = datetime.now()
# 获取一周中的第几天
day_of_week = today.weekday()
# 将数字转换为星期几的字符串
days = ["星期一", "星期二", "星期三", "星期四", "星期五", "星期六", "星期日"]
day_name = days[day_of_week]
print(f"今天是{day_name},在一周中是第{day_of_week + 1}天")- 说明
weekday()方法返回的整数范围是[0, 6],其中 0 表示星期一,6 表示星期日。如果需要将数字转换为星期几的字符串,
可以使用一个包含星期几名称的列表,通过索引获取对应的名称。
如果不需要下标转化的话,我觉得还是
isoweekday()更方便
说明: 返回一周中的第几天,与
weekday()类似,但返回值范围是
[1, 7],其中 1 表示星期一,7 表示星期日。
from datetime import datetime
# 获取当前日期
now = datetime.now()
# 获取一周中的第几天(ISO 标准)
day_of_week = now.isoweekday()
print("ISO 标准的一周中的第几天:", day_of_week)5_4、时间处理例题
P5707 【深基2.例12】上学迟到
- 题目描述
学校和 yyy 的家之间的距离为 s 米,而 yyy 以 v 米每分钟的速度匀速走向学校。
在上学的路上,yyy 还要额外花费 10 分钟的时间进行垃圾分类。
学校要求必须在上午 8:00到达,请计算在不迟到的前提下,yyy 最晚能什么时候出门。
由于路途遥远,yyy 可能不得不提前一点出发,但是提前的时间不会超过一天。
- 输入格式
一行两个正整数 s,v,分别代表路程和速度。
- 输出格式
输出一个 24小时制下的时间,代表 yyy 最晚的出发时间。
输出格式为 HH:MM,分别代表该时间的时和分。必须输出两位,不足前面补 0。
- 输入输出样例
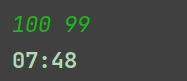
- 输入 :100 99
- 输出: 07:48
代码实现:
pythonfrom datetime import datetime,timedelta # 接收输入 s, v = map(int, input().split()) if s % v == 0: t = s // v # 没有余数,刚好除尽 else: t = s // v + 1 # 有余数就得多加一分钟 # 10分钟垃圾分类时间去除掉,那么计算中可以不携带,就算成7点50 # 随便设置一个 7点50的datetime t1 = datetime(year=2024,month=10,day= 24,hour=7,minute=50) # 设置一个timedelta,时间设置为上面算出来的t,即为上学需要的用时 t2 = timedelta(minutes=t) # 那么t1 - t2求出来的datetime就是最晚出发时间 t3 = t1 - t2 # 把datetime改变成输出的样式的字符串 t4 = t3.strftime("%H:%M") print(t4)输入示例输入检测:
六、手写next_permutation
背景:由于洛谷的 P1088 [NOIP2004 普及组] 火星人 这个问题,
用 python 的
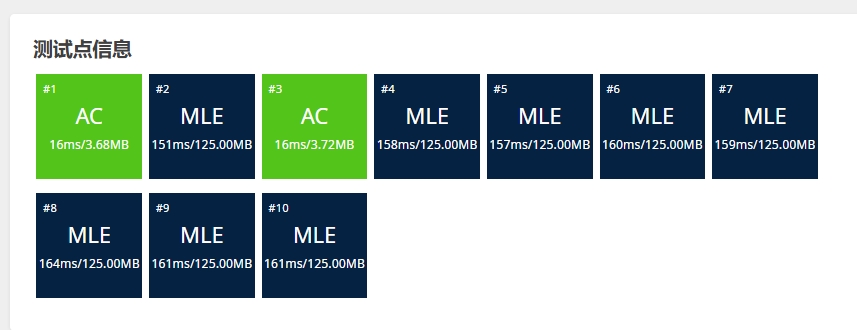
itertools.permutations去实现会导致内存过大MLE, 下面是这个版本的代码和提交结果:pythonfrom itertools import permutations n = int(input()) # 表示火星人手指的数目 m = int(input()) # 表示要加上去的小整数 # 下一行是 1 到 n 这 n 个整数的一个排列,用空格隔开,表示火星人手指的排列顺序 start_finger = tuple(map(int,input().split())) perms = [*permutations(range(1, n + 1))] start_num = perms.index(start_finger) + 1 # print(start_num) end_num = start_num + m for i in perms[end_num - 1]: print(i,end = " ")提交洛谷结果:
可见,像我那样
permutations(range(1, n + 1))一下子生成全排列存起来,n小还说可以,当n一下子巨大的时候,存的东西就变得巨大...从而我去搜寻
c/c++是怎么解决的 :因为有个
next_permutation, 可以不用存储全排列,搜寻下一个排列数,代码变得如此简洁高效...
但是 python 又没有类似的这些方法可以用 ....
从而我打算用 python 手写一个 next_permutation 来解决这个问题 :
💡 思路:
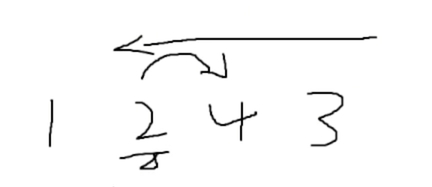
假设 我们针对的是
1 2 3 4这个序列它显然就是排列数里的第一位,然后排列数的最后一位就是
4 3 2 1先不说深层的什么东西,我们可以显然看到的是,第一位是单调递增,第二位是单调递减
(在这也不解释步骤原理,先掌握可以写出来)
示例序列 :
1 2 4 3目的: 寻找它的下一个排列数
- 第一步 : 从后往前查找第一个不是递增的元素
从后往前找,3 --> 4 是递增的,4 --> 2 是递减的,那么 2就是我们要找的那个
“从后往前查找第一个不是递增的元素” ,这名字太长了,我们称它为
第一个下降点第二步:从后向前查找第一个大于 arr[i] 的元素(与下降点交换)
也就是从3开始往前找,找第一个大于 2 的元素,那 3 不就是了么!
第三步:交换 “第一个下降点” 和 “ 交换点 ”
第四步:反转 下降点位置的后面的所有元素
代码实现:
pythondef next_permutation(arr): # 从后往前查找第一个不是递增的元素 # 1. 寻找“第一个下降点” i = len(arr)-2 while i >= 0 and arr[i] >= arr[i + 1]: i -= 1 # 向前遍历 # 上面 i < 0 了 也会跳出while # 如果已经是最后一个排列,则返回 False if i == -1: return False # 2. 寻找“交换点” # 从后向前查找第一个大于 arr[i] 的元素 j = len(arr) - 1 while arr[j] <= arr[i]: j -= 1 # 3. 交换“第一个下降点”和“交换点” # 交换这两个元素 arr[i], arr[j] = arr[j], arr[i] # 4. 反转 i 之后的所有元素 arr[i + 1:] = reversed(arr[i + 1:]) return True所以题目完整代码可以如下:
pythondef next_permutation(arr): # 从后往前查找第一个不是递增的元素 # 1. 寻找“第一个下降点” i = len(arr)-2 while i >= 0 and arr[i] >= arr[i + 1]: i -= 1 # 向前遍历 # 上面 i < 0 了 也会跳出while # 如果已经是最后一个排列,则返回 False if i == -1: return False # 2. 寻找“交换点” # 从后向前查找第一个大于 arr[i] 的元素 j = len(arr) - 1 while arr[j] <= arr[i]: j -= 1 # 3. 交换“第一个下降点”和“交换点” # 交换这两个元素 arr[i], arr[j] = arr[j], arr[i] # 4. 反转 i 之后的所有元素 arr[i + 1:] = reversed(arr[i + 1:]) return True n = int(input()) # 表示火星人手指的数目 m = int(input()) # 表示要加上去的小整数 # 下一行是 1 到 n 这 n 个整数的一个排列,用空格隔开,表示火星人手指的排列顺序 start_finger = [*map(int,input().split())] for i in range(m): next_permutation(start_finger) for j in start_finger: print(j,end=" ")第二份代码的提交结果如下:
七、gcd & lcm
两个数的 最大公约数(GCD)和最小公倍数(LCM)
import math
# 定义两个数
a = 12
b = 18
# 求最大公约数
gcd = math.gcd(a, b)
print("最大公约数是:", gcd)
# 求最小公倍数
lcm = abs(a * b) // gcd
print("最小公倍数是:", lcm)三个数的 最大公约数(GCD)和最小公倍数(LCM)
import math
# 定义三个数
a = 12
b = 18
c = 24
# 求最大公约数
gcd = math.gcd(math.gcd(a, b), c)
print("最大公约数是:", gcd)
# 求最小公倍数
def lcm(x, y):
return abs(x * y) // math.gcd(x, y)
lcm = lcm(lcm(a, b), c)
print("最小公倍数是:", lcm)八、二分查找
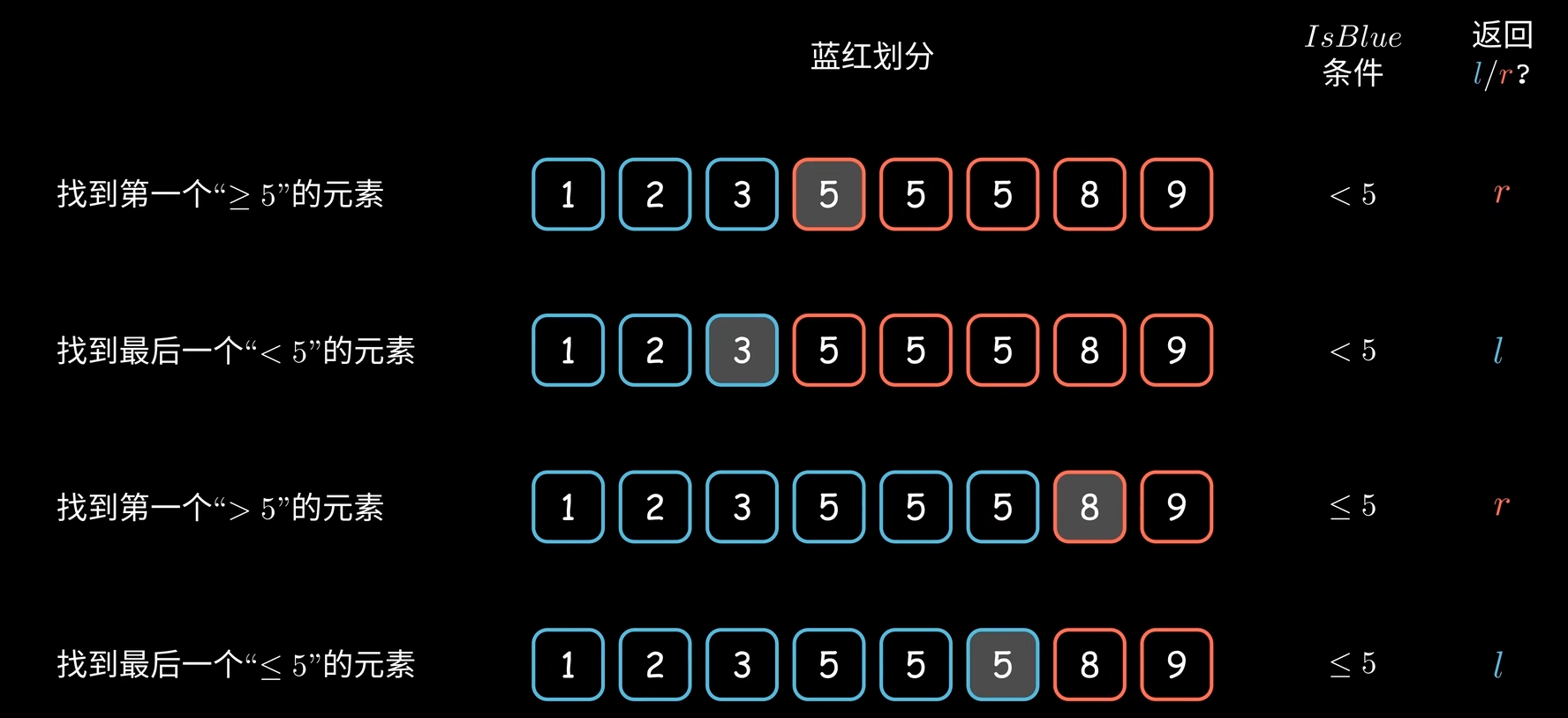
8.1 手写 lower_bound(arr,target)
推荐视频:五点七边の二分查找:https://www.bilibili.com/video/BV1d54y1q7k7/?spm_id_from=333.337.search-card.all.click&vd_source=2fbb4b17075136a98e03423a799add2c
# arr 1 2 3 5 5 5 8 9
nums = [1,2,3,5,5,5,8,9]
"""
第一种bound设计:
is_blue 指定为 arr[mid] < target
那么就会小于目标值的区域为蓝色区域
大于等于目标值的区域为红色区域
最后 return right 的话 对应的是 第一个 <= target (下标为 3 的 5)
最后 return left 的话 对应的是 最后一个 < target (下标为 2 的 3)
"""
def lower_bound1(arr,target,ori):
n = len(arr)
left = -1
right = n
while left + 1 != right:
mid = (left+right)//2
if arr[mid] < target:
left = mid
else:
# arr[mid] >= target
right = mid
if ori=="left":
return left
elif ori=="right":
return right
"""
第二种bound设计
is_blue 指定为 arr[mid] <= target
那么就会小于等于目标值为蓝色区域
大于目标值的区域为红色区域
最后 return right的话 对应的是 第一个 > target 的 (下标为 6 的 8)
最后 return left 的话 对应的是 最后一个 <= target 的 (下标为 5 的 5)
"""
def lower_bound2(arr,target,ori):
n = len(arr)
left = -1
right = n
while left + 1 != right:
mid = (left+right)//2
if arr[mid] <= target:
left = mid
else:
# arr[mid] > target
right = mid
if ori == "left":
return left
elif ori == "right":
return right
"""
1.最后 return right 的话 对应的是 第一个 <= target
2.最后 return left 的话 对应的是 最后一个 < target
"""
print("值为",nums[lower_bound1(nums, 5,"right")],"下标为",lower_bound1(nums, 5,"right")) # 值为 5 下标为 3
print("值为",nums[lower_bound1(nums, 5,"left")],"下标为",lower_bound1(nums, 5,"left")) # 值为 3 下标为 2
"""
最后 return right的话 对应的是 第一个 > target 的
最后 return left 的话 对应的是 最后一个 <= target 的
"""
print("值为",nums[lower_bound2(nums,5,"right")],"下标为",lower_bound2(nums,5,"right")) # 值为 8 下标为 6
print("值为",nums[lower_bound2(nums,5,"left")],"下标为",lower_bound2(nums,5,"left")) # 值为 5 下标为 58.2 调用 bisect
from bisect import bisect_left,bisect_right
nums = [1,2,3,5,5,5,8,9]
print("下标为",bisect_left(nums,5)) # 下标为 3 (第一个小于等于)
print("下标为",bisect_right(nums,5)) # 下标为 6 (第一个大于)- 注意:二分查找要基于有序的数组!!!(无序数组使用二分前需要先
sort())
九、回溯算法
- 回溯三问
- 当前操作是什么?
- 子问题是什么?
- 下一个子问题是什么?
9.0 pre_从多重循环到回溯
- 示例代码:
letter_map = ['','','abc','def','ghi','jkl','mno','pqrs','tuv','wxyz']
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
n = len(digits)
# 特例
if n == 0:
return []
ans = [] # 存储全部答案(所有叶子节点的值)
path = [''] * n # 存储单次路径(单次路径的值)
# 深搜代码
def dfs(i):
# 边界
if i == n:
# 递归到了叶子节点,记录答案
return ans.append("".join(path))
# 非边界
for c in letter_map[int(digits[i])]:
# 遍历第i个digits所能对应到的字母
path[i] = c
# 因为会遍历到全部字母
# 任意取一个字母进入path后沿着"这条路径"深搜
dfs(i+1) # 子问题
# 递归入口
dfs(0)
return ans- 本题的递归搜索树如下:(感受增量构造答案的过程)
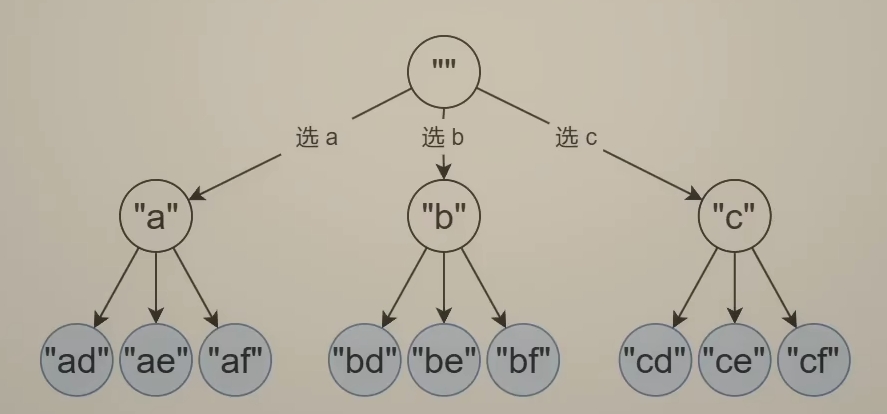
9.1 子集型回溯
- 第一种思路:站在 输入 的角度思考
- 每个数可以在子集中(选)
- 每个数也可以不在子集中(不选)
- 叶子节点是答案
- 示例代码:(子集型回溯模板一)
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
ans = [] # 全部
path = [] # 单次
# 深搜代码
def dfs(i):
# 边界
if i == n:
# 到达叶子节点,记录答案
ans.append(path.copy())
return
# 非边界
# 不选当前数
dfs(i+1)
# 选当前数
path.append(nums[i])
# 深搜
dfs(i+1)
path.pop() # 恢复现场(回溯核心)
# 递归入口
dfs(0)
return ans- 递归搜索树如下:(选/不选的思路)
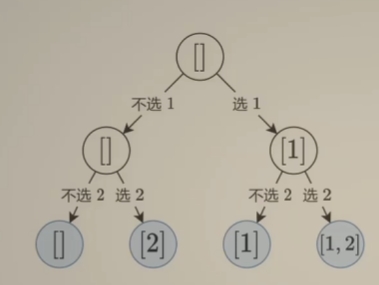
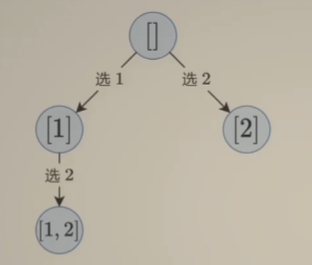
- 第二种思路:站在 答案 的角度思考
- 枚举第一个数选谁
- 枚举第二个数选谁
- 每个节点都是答案
- 注意:[1,2] 和 [2,1] 是重复的子集,为了避免重复,下一个数应(下标)大于当前选择的数
- 示例代码:(子集型回溯模板二)
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
ans = []
path = []
def dfs(i):
# 每一个节点都是答案
ans.append(path.copy())
if i == n:
return
# 遍历当前位置选什么
for j in range(i,n):
path.append(nums[j])
dfs(j+1) # 为了避免重复,下一个数应(下标)大于当前选择的数
path.pop() # 恢复现场
dfs(0)
return ans- 递归搜索树如下:(每个节点都是答案)